Question

【题目】如图，在四棱锥P-ABCD中，PA⊥平面ABCD，E为PA的中点，F为BC的中点，底面ABCD是菱形，对角线AC，BD交于点O．求证：

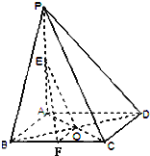
（1）平面EFO∥平面PCD；

（2）平面PAC⊥平面PBD．

Answer 1

【答案】（1）见解析（2）见解析

【解析】

（1）由题意知，EO∥PC，由线面平行的判定定理得到EO∥平面PCD，同理可证，FO∥平面PCD，再由面面平行的判定定理，即得证平面EFO∥平面PCD．

（2）由于PA⊥平面ABCD，得到PA⊥BD，再由已知得到BD⊥平面PAC，由面面垂直的判定定理，即得证平面PAC⊥平面PBD．

（1）因为E为PA的中点，O为AC的中点，所以EO∥PC

又EO平面PCD，PC平面PCD，所以EO∥平面PCD

同理可证，FO∥平面PCD，又EO∩FO＝O

所以，平面EFO∥平面PCD．

（2）因为PA⊥平面ABCD，BD平面ABCD，所以PA⊥BD

因为底面ABCD是菱形，所以AC⊥BD，又PA∩AC＝A

所以BD⊥平面PAC

又BD平面PBD，所以平面PAC⊥平面PBD．