题目内容
【题目】已知动点M(x,y)满足![]() ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.
(1)求E的标准方程;
(2)过点F(1,0)作直线交曲线E于P,Q两点,交![]() 轴于R点,若
轴于R点,若![]() ,证明:
,证明:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)-4.
;(2)-4.
【解析】分析:(Ⅰ)由![]() ,根据椭圆的定义可得点
,根据椭圆的定义可得点![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,可求得
为焦点的椭圆,可求得![]() ,从而可得曲线
,从而可得曲线![]() 的方程;(II)设
的方程;(II)设![]() ,由
,由![]() ,点
,点![]() 在曲线
在曲线![]() 上可得
上可得![]() …,①同理可得
…,①同理可得![]() …,②,由①②可得
…,②,由①②可得![]() 是方程
是方程![]() 的两个根,
的两个根,![]() 为定值
为定值![]() .
.
详解:(Ⅰ)由![]() ,
,
可得点M(x,y)到定点A(﹣1,0),B(1,0)的距离等于之和等于![]() .
.
且AB![]() ,所以动点N的轨迹是以C(﹣1,0),A(1,0)为焦点的椭圆,
,所以动点N的轨迹是以C(﹣1,0),A(1,0)为焦点的椭圆,
且长轴长为![]() ,焦距2c=2,所以,c=1,b=1,曲线E的方程为:
,焦距2c=2,所以,c=1,b=1,曲线E的方程为:![]() ;
;
(Ⅱ)法1:设P(x1,y1),Q(x2,y2),R(0,y0),
由![]() ,(x1,y1﹣y0)=λ1(1﹣x1,﹣y1),∴
,(x1,y1﹣y0)=λ1(1﹣x1,﹣y1),∴![]() ,
,
∵过点F(1,0)作直线l交曲线E于P,∴![]() ,
,
∴![]() …①
…①
同理可得:![]() …②
…②
由①②可得λ1、λ2是方程x2+4x+2﹣2y02=0的两个根,∴λ1+λ2为定值﹣4.
法2:依题意得![]() 的斜率一定存在,设斜率为k,
的斜率一定存在,设斜率为k,
则直线方程为![]() 代入椭圆方程得:
代入椭圆方程得:![]()
设![]() ,则
,则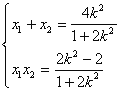 ,
,
由![]() 得:
得:![]() 得
得![]()
同理得:![]()
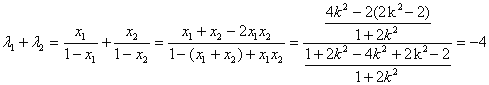
则![]() 为定值。
为定值。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目