题目内容
【题目】已知点![]() ,
, ![]() 为椭圆
为椭圆![]() :
:![]() 上异于点A,B的任意一点.
上异于点A,B的任意一点.
(Ⅰ)求证:直线![]() 、
、![]() 的斜率之积为
的斜率之积为![]() -;
-;
(Ⅱ)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)见解析(2)![]()
【解析】试题分析:(Ⅰ)设![]() ,并用其坐标表示斜率,通过斜率之积,结合点在椭圆上,化简可得直线
,并用其坐标表示斜率,通过斜率之积,结合点在椭圆上,化简可得直线![]() 、
、![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅱ)设点![]() 取MN的中点H,则
取MN的中点H,则![]() ,则|
,则|![]() 可转化为
可转化为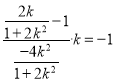 ,联立直线与椭圆,结合韦达定理建立关于斜率k的方程,求解即可.
,联立直线与椭圆,结合韦达定理建立关于斜率k的方程,求解即可.
试题解析:(I)设点![]() ,
,![]() ,则
,则
![]() ,即
,即![]()
![]()
![]()
![]()
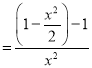
![]()
故得证.
(II)假设存在直线![]() 满足题意.
满足题意.
显然当直线斜率不存在时,直线与椭圆![]() 不相交.
不相交.
①当直线![]() 的斜率
的斜率![]() 时,设直线
时,设直线![]() 为:
为:![]()
联立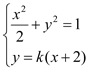 ,化简得:
,化简得:![]()
由![]() ,解得
,解得![]()
设点![]() ,
,![]() ,则
,则
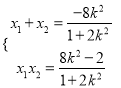
![]()
![]()
取![]() 的中点
的中点![]() ,则
,则![]() ,则
,则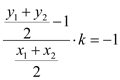
即 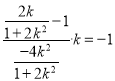 ,化简得
,化简得![]() ,无实数解,故舍去.
,无实数解,故舍去.
②当![]() 时,
时, ![]() 为椭圆
为椭圆![]() 的左右顶点,显然满足
的左右顶点,显然满足![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
综上可知,存在直线![]() 满足题意,此时直线
满足题意,此时直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
