题目内容
【题目】如图,已知梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,
为矩形, ![]() ,平面
,平面![]() 平面
平面![]() .
.
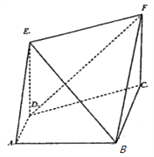
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】试题分析:(1)利用空间向量证明线面平行,一般转化为对应平面法向量与直线垂直,先建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,根据向量数量积证明垂直,最后根据线面平行判定定理证明,(2)求二面角,一般利用空间向量进行求解,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与向量夹角之间相等或互补
关系求解(3)研究线面角,一般利用空间向量进行列式求解参数,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据线面角与向量夹角之间互余关系列式求解参数.
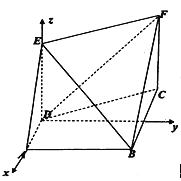
试题解析:(Ⅰ)证明:取![]() 为原点,
为原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,如图,则
轴建立空间直角坐标系,如图,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
∴ 不妨设
不妨设![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)解:∵![]() ,
, ![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
∴ 不妨设
不妨设![]() ,
,
∴ ,
,
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
(Ⅲ)设![]()
![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵平面![]() 的法向量
的法向量![]() ,
,
∴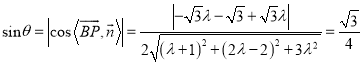 ,
,
∴![]() ,
,
∴![]() 或
或![]() .
.
当![]() 时,
时,  ,∴
,∴![]() ;
;
当![]() 时,
时,  ,∴
,∴![]() .
.
综上, ![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某农科所记录了5组昼夜温差与100颗种子发芽数,得到如下资料:
组号 | 1 | 2 | 3 | 4 | 5 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求出线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是第1组与第5组的两组数据,请根据第2组至第4组的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: ,
,![]() )
)
【题目】如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,![]() .
.

(1)证明: A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
【题目】为了增强消防安全意识,某中学对全体学生做了一次消防知识讲座,从男生中随机抽取50人,从女生中随机抽取70人参加消防知识测试,统计数据得到如下列联表:
优秀 | 非优秀 | 总计 | |
男生 | 15 | 35 | 50 |
女生 | 30 | 40 | 70 |
总计 | 45 | 75 | 120 |
(Ⅰ)试判断是否有![]() 的把握认为消防知识的测试成绩优秀与否与性别有关;
的把握认为消防知识的测试成绩优秀与否与性别有关;
附:
K2=![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅱ)为了宣传消防安全知识,从该校测试成绩获得优秀的同学中采用分层抽样的方法,随机选出6名组成宣传小组,现从这6人中随机抽取2名到校外宣传,求到校外宣传的同学中至少有1名是男生的概率.
