题目内容
【题目】如图,在直角梯形ABCP中,CP∥AB,CP⊥CB,![]() ,CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥面ABCD.
,CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥面ABCD.

(1)求证:平面PAD⊥平面PCD;
(2)若E是PC的中点,求三棱锥D﹣PEB的体积.
【答案】(1)见解析;(2)![]()
【解析】
(1)由PD⊥底面ABCD,得PD⊥AD.结合CP∥AB,CP⊥CB,AB=BC,可得ABCD为正方形,得到AD⊥CD,则AD⊥底面PCD,再由面面垂直的判定得平面PAD⊥底面PCD;
(2)由PD=DC,E是PC的中点,得DE⊥PC.结合(1)知AD⊥底面PCD,得AD⊥DE.从而得到BC⊥DE.进一步得到DE⊥底面PBC.然后求解直角三角形得到三角形PBC的面积代入体积公式得答案.
(1)证明:∵PD⊥底面ABCD,∴PD⊥AD.
又由于CP∥AB,CP⊥CB,AB=BC,∴ABCD为正方形,
∴AD⊥CD,又PD∩CD=D,故AD⊥底面PCD,
∵AD平面PAD,∴平面PAD⊥底面PCD;
(2)解:∵PD=DC,E是PC的中点,∴DE⊥PC.
由(1)知有AD⊥底面PCD,∴AD⊥DE.
由题意得AD∥BC,故BC⊥DE.
于是,由BC∩PC=C,可得DE⊥底面PBC.
∴DE=![]() ,PC=2
,PC=2![]() ,
,
又∵AD⊥底面PCD,∴AD⊥CP,
∵AD∥BC,∴AD⊥BC.
∴![]() =
=![]() =
=![]() ×
×![]() =
=![]()
∴![]() =
=![]() ×DE×
×DE×![]() =
=![]() .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
【题目】北京市某年11月1日—20日监测最高最低温度及差值数据如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高温度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低温度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的频率分布表及频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;

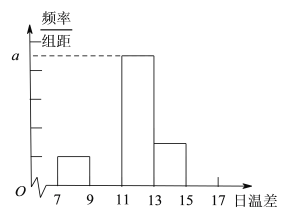
(Ⅱ)从日温差大于等于![]() 的这些天中,随机选取2天.求这两天中至少有一天的温差在区间
的这些天中,随机选取2天.求这两天中至少有一天的温差在区间![]() 内的概率.
内的概率.