题目内容
12.讨论方程$\sqrt{|1-x|}$=kx的实数根的个数.分析 作函数f(x)=$\sqrt{|1-x|}$与函数g(x)=kx的图象,从而化方程的根的个数为图象的交点的个数,从而解得.
解答 解:作函数f(x)=$\sqrt{|1-x|}$与函数g(x)=kx的图象如下,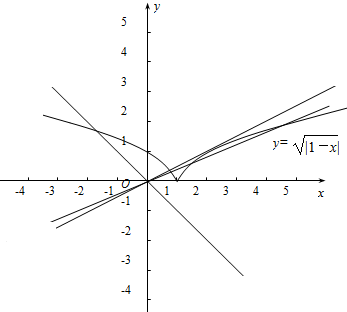 ,
,
当x>1时,f(x)=$\sqrt{x-1}$,f′(x)=$\frac{1}{2\sqrt{x-1}}$,
设切点为(x,y),则$\frac{\sqrt{x-1}}{x}$=$\frac{1}{2\sqrt{x-1}}$,
解得,x=2,故f′(2)=$\frac{1}{2}$;
故当k≤0或k>$\frac{1}{2}$时,函数f(x)=$\sqrt{|1-x|}$与函数g(x)=kx的图象有一个交点,
故方程$\sqrt{|1-x|}$=kx的实数根的个数为1;
当k=$\frac{1}{2}$时,函数f(x)=$\sqrt{|1-x|}$与函数g(x)=kx的图象有两个交点,
故方程$\sqrt{|1-x|}$=kx的实数根的个数为2;
当0<k<$\frac{1}{2}$时,函数f(x)=$\sqrt{|1-x|}$与函数g(x)=kx的图象有三个交点,
故方程$\sqrt{|1-x|}$=kx的实数根的个数为3.
点评 本题考查了方程的根与函数的图象的交点的关系应用及分类讨论的思想应用,同时考查了数形结合.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
3.等差数列{an}中,a5=4,a9=10,则a13=( )
| A. | 25 | B. | 16 | C. | 14 | D. | 12 |
20.下列函数中,以π为周期的函数是( )
| A. | y=|sinx| | B. | y=sin|x| | C. | y=sinx | D. | y=$\frac{1}{2}$sinx |
7.数列{an}的前n项和Sn=n(n+1),则它的第n项an是( )
| A. | n | B. | n(n+1) | C. | 2n | D. | 2n |
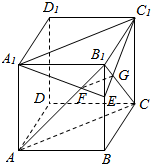 如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.
如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.