ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“χ¥®“Μ÷–ΈΣ―–ΨΩ―ß…ζΒΡ…μΧεΥΊ÷ ”κΩΈΆβΧε”ΐΕΆΝΕ ±ΦδΒΡΙΊœΒΘ§≥ι»Γ‘Ύ–Θ200Οϊ―ß…ζΒΡΩΈΆβΧε”ΐΕΆΝΕΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±ΦδΘ®ΒΞΈΜΘΚΖ÷÷”Θ©Ϋχ––Βς≤ιΘ§ΫΪ ’Φ·ΒΡ ΐΨίΖ÷≥…![]() Θ§
Θ§![]() ΝυΉιΘ§≤ΔΉς≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ®»γΆΦΘ©Θ§ΫΪ»’ΨυΩΈΆβΧε”ΐΕΆΝΕ ±Φδ≤ΜΒΆ”Ύ40Ζ÷÷”ΒΡ―ß…ζΤάΦέΈΣΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±Θ°
ΝυΉιΘ§≤ΔΉς≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ®»γΆΦΘ©Θ§ΫΪ»’ΨυΩΈΆβΧε”ΐΕΆΝΕ ±Φδ≤ΜΒΆ”Ύ40Ζ÷÷”ΒΡ―ß…ζΤάΦέΈΣΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±Θ°
ΩΈΆβΧε”ΐ≤Μ¥ο±ξ | ΩΈΆβΧε”ΐ¥ο±ξ | ΚœΦΤ | |
Ρ– |
| ||
š |
| ||
ΚœΦΤ |
Θ®1Θ©«κΗυΨί÷±ΖΫΆΦ÷–ΒΡ ΐΨίΧν–¥œ¬ΟφΒΡ![]() Ν–ΝΣ±μΘ§≤ΔΆ®ΙΐΦΤΥψ≈–Εœ «ΖώΡή‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ
Ν–ΝΣ±μΘ§≤ΔΆ®ΙΐΦΤΥψ≈–Εœ «ΖώΡή‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±”κ–‘±π”–ΙΊΘΩ
ΒΡ«ΑΧαœ¬»œΈΣΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±”κ–‘±π”–ΙΊΘΩ
Θ®2Θ©‘Ύ![]() ’βΝΫΉι÷–≤…»ΓΖ÷≤ψ≥ι―υΘ§≥ι»Γ6»ΥΘ§‘Ό¥”’β6Οϊ―ß…ζ÷–ΥφΜζ≥ι»Γ2»Υ≤ΈΦ”Χε”ΐ÷Σ ΕΈ ΨμΒς≤ιΘ§«σ’β2»Υ÷–“Μ»Υά¥Ή‘ΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±ΚΆ“Μ»Υά¥Ή‘ΓΑΩΈΆβΧε”ΐ≤Μ¥ο±ξΓ±ΒΡΗ≈¬ Θ°
’βΝΫΉι÷–≤…»ΓΖ÷≤ψ≥ι―υΘ§≥ι»Γ6»ΥΘ§‘Ό¥”’β6Οϊ―ß…ζ÷–ΥφΜζ≥ι»Γ2»Υ≤ΈΦ”Χε”ΐ÷Σ ΕΈ ΨμΒς≤ιΘ§«σ’β2»Υ÷–“Μ»Υά¥Ή‘ΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±ΚΆ“Μ»Υά¥Ή‘ΓΑΩΈΆβΧε”ΐ≤Μ¥ο±ξΓ±ΒΡΗ≈¬ Θ°
ΗΫ≤ΈΩΦΙΪ Ϋ”κΘΚ![]()
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
ΓΨ¥πΑΗΓΩΘ®1Θ©≤ΜΡήΘΜΘ®2Θ©![]() .
.
ΓΨΫβΈωΓΩΖ÷ΈωΘΚ(1)ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ,ΦΤΥψΕ‘”ΠΒΡ ΐΨί,Χν–¥![]() Ν–ΝΣ±μ,ΦΤΥψΙέ≤β÷Β
Ν–ΝΣ±μ,ΦΤΥψΙέ≤β÷Β![]() ,Ε‘’’ ΐ±μΒΟ≥ωΫα¬έ;
,Ε‘’’ ΐ±μΒΟ≥ωΫα¬έ;
(2)ΗυΨίΖ÷≤ψ≥ι―υ“‘ΦΑΝ–ΨΌΖ®«σ≥ωΕ‘”ΠΒΡΜυ±Ψ ¬Φΰ ΐ,ΦΤΥψΕ‘”ΠΒΡΗ≈¬ ÷Β.
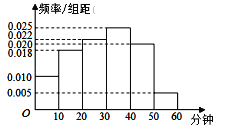
œξΫβΘΚΘ®1Θ©”…Χβ“βΒΟΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±»Υ ΐΘΚ200ΓΝ[Θ®0.02+0.005Θ©ΓΝ10]=50Θ§
‘ρ≤Μ¥ο±ξ»Υ ΐΈΣ150Θ§
ΓύΝ–ΝΣ±μ»γœ¬ΘΚ
ΩΈΆβΧε”ΐ≤Μ¥ο±ξ | ΩΈΆβΧε”ΐ¥ο±ξ | ΚœΦΤ | |
Ρ– | 60 | 30 | 90 |
š | 90 | 20 | 110 |
ΚœΦΤ | 150 | 50 | 200 |
Γύk2=![]() =
=![]() Γ÷6.060ΘΦ6.635Θ§
Γ÷6.060ΘΦ6.635Θ§
Γύ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.01ΒΡ«ΑΧαœ¬ΟΜ”–άμ”…Θ®Μρ≤ΜΡήΘ©»œΈΣΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±”κ–‘±π”–ΙΊ.
Θ®2Θ©”…Χβ“β‘Ύ[0Θ§10Θ©Θ§[40Θ§50Θ©Ζ÷±π”–20»ΥΘ§40»ΥΘ§
‘ρ≤…»ΓΖ÷≤ψ≥ι―υ‘Ύ[0Θ§10Θ©≥ι»ΓΒΡ»Υ ΐΈΣΘΚ![]() »ΥΘ§
»ΥΘ§
‘Ύ[40Θ§50Θ©≥ι»ΓΒΡ»Υ ΐΈΣΘΚ![]() »ΥΘ§
»ΥΘ§
[0Θ§10Θ©≥ι»ΓΒΡ»ΥΈΣAΘ§BΘ§‘Ύ[40Θ§50Θ©≥ι»ΓΒΡ»ΥΈΣaΘ§bΘ§cΘ§dΘ§
¥”’β6»Έ÷–ΥφΜζ≥ι»Γ2»ΥΒΡ«ιΩωΈΣΘΚABΘ§AaΘ§AbΘ§AcΘ§AdΘ§BaΘ§BbΘ§BcΘ§BdΘ§abΘ§acΘ§adΘ§bcΘ§bdΘ§cdΙ≤15÷÷Θ§
2»Υ÷–“Μ»Υά¥Ή‘ΓΑΩΈΆβΧε”ΐ¥ο±ξΓ±ΚΆ“Μ»Υά¥Ή‘ΓΑΩΈΆβΧε”ΐ≤Μ¥ο±ξΓ±Ι≤”–ΘΚAaΘ§AbΘ§AcΘ§AdΘ§BaΘ§BbΘ§BcΘ§BdΙ≤8÷÷Θ§
Γύ![]() Θ°
Θ°

 ±Η’Ϋ÷–ΩΦΚ°ΦΌœΒΝ–¥πΑΗ
±Η’Ϋ÷–ΩΦΚ°ΦΌœΒΝ–¥πΑΗ