题目内容
【题目】设常数a≥0,函数f(x)= ![]() .
.
(1)若a=4,求函数y=f(x)的反函数y=f﹣1(x);
(2)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由.
【答案】
(1)解:∵a=4,
∴ ![]()
∴ ![]() ,
,
∴ ![]() ,
,
∴调换x,y的位置可得 ![]() ,x∈(﹣∞,﹣1)∪(1,+∞).
,x∈(﹣∞,﹣1)∪(1,+∞).
(2)解:若f(x)为偶函数,则f(x)=f(﹣x)对任意x均成立,
∴ ![]() =
= ![]() ,整理可得a(2x﹣2﹣x)=0.
,整理可得a(2x﹣2﹣x)=0.
∵2x﹣2﹣x不恒为0,
∴a=0,此时f(x)=1,x∈R,满足条件;
若f(x)为奇函数,则f(x)=﹣f(﹣x)对任意x均成立,
∴ ![]() =﹣
=﹣ ![]() ,整理可得a2﹣1=0,
,整理可得a2﹣1=0,
∴a=±1,
∵a≥0,
∴a=1,
此时f(x)= ![]() ,满足条件;
,满足条件;
当a>0且a≠1时,f(x)为非奇非偶函数
综上所述,a=0时,f(x)是偶函数,a=1时,f(x)是奇函数.当a>0且a≠1时,f(x)为非奇非偶函数
【解析】(1)根据反函数的定义,即可求出,(2)利用分类讨论的思想,若为偶函数求出a的值,若为奇函数,求出a的值,问题得以解决.
【考点精析】利用函数的奇偶性对题目进行判断即可得到答案,需要熟知偶函数的图象关于y轴对称;奇函数的图象关于原点对称.

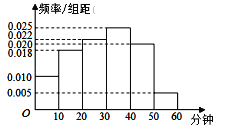
【题目】银川一中为研究学生的身体素质与课外体育锻炼时间的关系,抽取在校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() ,
,![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
课外体育不达标 | 课外体育达标 | 合计 | |
男 |
| ||
女 |
| ||
合计 |
(1)请根据直方图中的数据填写下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
(2)在![]() 这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
附参考公式与:![]()
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|