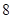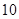题目内容
(本小题9分) 已知数列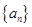 的前
的前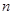 项和
项和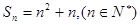 (1)求数列
(1)求数列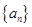 的通项公式;(2)令
的通项公式;(2)令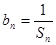 ,记数列{
,记数列{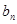 }的前
}的前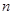 项和为
项和为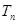 ,求
,求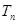 。
。
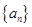 的前
的前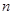 项和
项和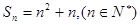 (1)求数列
(1)求数列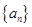 的通项公式;(2)令
的通项公式;(2)令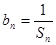 ,记数列{
,记数列{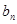 }的前
}的前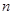 项和为
项和为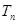 ,求
,求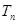 。
。(1)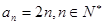 (2)
(2)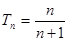
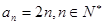 (2)
(2)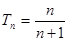
本试题主要是考查了数列的前n项和与数列的通项公式的之间的关系的转换,以及利用数列的通项公式的特点进行求和的综合运用。主要是裂项求和的运用。
(1)对于n分别取1,和n大于等于2时,得到数列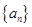 的通项公式。
的通项公式。
(2)利用第一问的结论,得到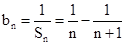 ,采用裂项的思想,求解数列的前n项和的综合运用问题。
,采用裂项的思想,求解数列的前n项和的综合运用问题。
(1)对于n分别取1,和n大于等于2时,得到数列
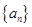 的通项公式。
的通项公式。(2)利用第一问的结论,得到
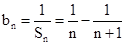 ,采用裂项的思想,求解数列的前n项和的综合运用问题。
,采用裂项的思想,求解数列的前n项和的综合运用问题。
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
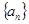 是等差数列,且
是等差数列,且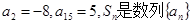 的前n项和,则 ( )
的前n项和,则 ( )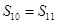 ;
;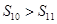 ;
; ;
;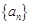 是各项均为正数的等差数列.
是各项均为正数的等差数列.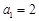 ,且
,且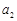 ,
,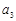 ,
,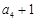 成等比数列,求数列
成等比数列,求数列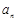 ;
;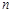 和为
和为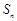 ,设
,设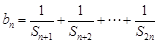 ,若对任意的
,若对任意的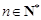 ,不等式
,不等式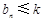 恒成立,求实数
恒成立,求实数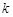 的最小值;
的最小值;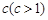 的不同次幂,求证:数列
的不同次幂,求证:数列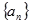 是公差不为零的等差数列,
是公差不为零的等差数列,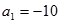 ,且
,且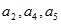 成等比数列.
成等比数列.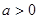 ,求数列
,求数列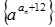 的前n项和
的前n项和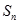 .
.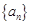 满足:
满足: ,
,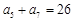 .
.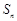 .
.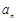 及
及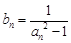 (
(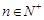 ),求数列
),求数列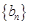 的前n项和
的前n项和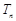 .
.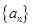 的前n项和为
的前n项和为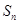 ,若
,若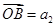
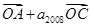 ,且A、B、C三点共线(O为该直线外一点),则
,且A、B、C三点共线(O为该直线外一点),则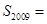 _________.
_________.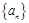 的公差不为零,
的公差不为零,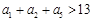 ,且
,且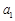 、
、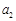 、
、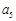 成等比数
成等比数 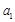 的取值范围为 .
的取值范围为 .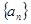 中,
中,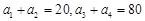 ,则
,则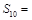 ________
________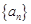 中,若
中,若 ,则
,则 ( )
( )