题目内容
3.已知2x=3y=6z≠1,求证:$\frac{1}{x}$$+\frac{1}{y}$=$\frac{1}{z}$.分析 由2x=3y=6z≠1,用对数表示出x、y、z,再利用换底公式计算即可.
解答 解:设2x=3y=6z=k≠1,
∴x=log2k,y=log3k,z=log6k;
∴$\frac{1}{x}$=logk2,$\frac{1}{y}$=logk3,$\frac{1}{z}$=logk6,
∴$\frac{1}{x}$$+\frac{1}{y}$=logk2+logk3=logk6=$\frac{1}{z}$
故问题得以证明.
点评 本题考查了指数与对数的应用问题,也考查了换底公式的应用问题,是基础题目.

练习册系列答案
相关题目
14.函数y=f(x)在[-2,2]上的图象如图所示,则此函数的最小值、最大值分别是( )
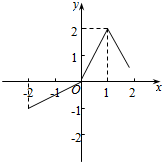
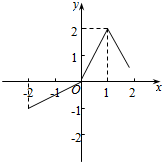
| A. | f(-2),0 | B. | 0,2 | C. | f(-2),2 | D. | f(2),2 |