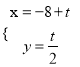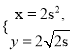题目内容
【题目】在正方体ABCD﹣A1B1C1D1中,M、N分别为CD和A1D1的中点,那么异面直线AM与BN 所成的角是( )
A.90°
B.60°
C.45°
D.30°
【答案】A
【解析】解:取C1D1的中点P,取PD1的中点Q,连接BQ,NQ
根据正方体的结构特征
可得AM∥A1P,且NQ∥A1P,
故NQ∥AM,
则∠BNQ即为异面直线AM与BN 所成的角,
∵在△BC1Q中,BQ= ![]() =
= ![]()
∴在△BNQ中,NQ= ![]() ,
,
BN= ![]() ,
,
∴BN2+NQ2=BQ2
∴∠BNQ=90°
所以答案是90°.
故选A.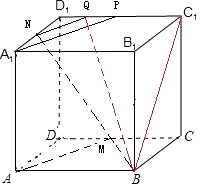
【考点精析】根据题目的已知条件,利用异面直线及其所成的角的相关知识可以得到问题的答案,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

练习册系列答案
相关题目
【题目】通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
男 | 女 | 总计 | |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() ,算得
,算得 ![]()
参照独立性检验附表,得到的正确结论是( )
A.有99%的把握认为“选择过马路的方式与性别有关”
B.有99%的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”