��Ŀ����
�������壺��m-
��x��m+
������mΪ����������m������ʵ��x���������������{x}=m���ڴ˻����ϸ������й��ں���f��x��=|x-{x}|���ĸ����⣺
�ٺ���y=f��x���Ķ�����ΪR��ֵ��Ϊ[0��
]��
�ں���y=f��x����ͼ�����ֱ��x=
(k��Z)�Գƣ�
�ۺ���y=f��x����ż������
�ܺ���y=f��x����[-
��
]������������ ������ȷ������������
| 1 |
| 2 |
| 1 |
| 2 |
�ٺ���y=f��x���Ķ�����ΪR��ֵ��Ϊ[0��
| 1 |
| 2 |
�ں���y=f��x����ͼ�����ֱ��x=
| k |
| 2 |
�ۺ���y=f��x����ż������
�ܺ���y=f��x����[-
| 1 |
| 2 |
| 1 |
| 2 |
�٢ڢ�
�٢ڢ�
������������Ϊ�¶������⣬��ΪmΪ�������ʿ�ȡmΪ������������������о��������õ�������ͼ��IJ�ͼ�����ͼ������õ��𰸣�
���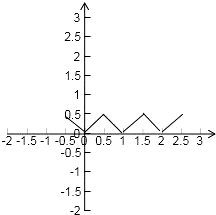 �⣺������x-{x}=x-m��f��x��=|x-{x}|=|x-m|��
�⣺������x-{x}=x-m��f��x��=|x-{x}|=|x-m|��
m=0ʱ��-
��x��
��f��x��=|x|��
m=1ʱ��1-
��x��1+
��f��x��=|x-1|��
m=2ʱ��2-
��x��2+
��f��x��=|x-2|��
��
����������ͼ����ͼ��ʾ����ͼ���֪��ȷ����Ϊ�٢ڢۣ�
�ʴ�Ϊ���٢ڢ�
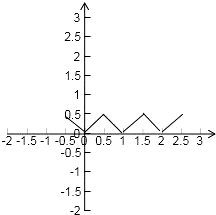 �⣺������x-{x}=x-m��f��x��=|x-{x}|=|x-m|��
�⣺������x-{x}=x-m��f��x��=|x-{x}|=|x-m|��m=0ʱ��-
| 1 |
| 2 |
| 1 |
| 2 |
m=1ʱ��1-
| 1 |
| 2 |
| 1 |
| 2 |
m=2ʱ��2-
| 1 |
| 2 |
| 1 |
| 2 |
��
����������ͼ����ͼ��ʾ����ͼ���֪��ȷ����Ϊ�٢ڢۣ�
�ʴ�Ϊ���٢ڢ�
�������������¶������⣬���麯�������ʣ��ɽ��ͼ������о����������ν��˼�룮

��ϰ��ϵ�д�
�����Ŀ