题目内容
给出定义:若m-
<x≤m+
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m,在此基础上给出下列关于函数f(x)=x-{x}的四个命题:
①y=f(x)的定义域是R,值域是(-
,
];
②点(k,0)(k∈Z)是y=f(x)的图象的对称中心;
③函数y=f(x)在(-
,
]上是增函数;
④函数y=f(x)的最小正周期为1;
则其中真命题是
| 1 |
| 2 |
| 1 |
| 2 |
①y=f(x)的定义域是R,值域是(-
| 1 |
| 2 |
| 1 |
| 2 |
②点(k,0)(k∈Z)是y=f(x)的图象的对称中心;
③函数y=f(x)在(-
| 1 |
| 2 |
| 3 |
| 2 |
④函数y=f(x)的最小正周期为1;
则其中真命题是
①④
①④
.分析:根据题意,先对函数化简,然后作出函数的图象,根据函数的图象可判断各个选项是否正确.
解答:解:由定义:m-
<x≤m+
(其中m为整数),得-
<x-m≤
,
据此可画出函数图象:
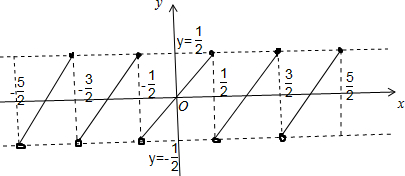
①∵对于任意实数x,函数f(x)都有意义,故函数的定义域为R,值域是(-
,
];
②∵(
,
)在图象上,(-
,-
)不在图象上,∴点(0,0)不是y=f(x)的图象的对称中心;②错;
③函数y=f(x)在(-
,
)上是增函数;③错;
④从图象的周期性变化来看,函数y=f(x)的最小正周期为1;
由此可选择①④.
故答案为:①④.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
据此可画出函数图象:

①∵对于任意实数x,函数f(x)都有意义,故函数的定义域为R,值域是(-
| 1 |
| 2 |
| 1 |
| 2 |
②∵(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
③函数y=f(x)在(-
| 1 |
| 2 |
| 1 |
| 2 |
④从图象的周期性变化来看,函数y=f(x)的最小正周期为1;
由此可选择①④.
故答案为:①④.
点评:本题为新定义题目,解题的关键是读懂定义内涵,尝试探究解决,属难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目