题目内容
(2011•昌平区二模)给出定义:若m-
<x≤m+
(其中m为整数),则m叫做离实数x最近的整数,记作{x}=m,在此基础上给出下列关于函数f(x)=x-{x}的四个命题:
①函数y=f(x)的定义域为R,最大值是
;②函数y=f(x)在[0,1]上是增函数;
③函数y=f(x)是周期函数,最小正周期为1;④函数y=f(x)的图象的对称中心是(0,0).
其中正确命题的序号是
| 1 |
| 2 |
| 1 |
| 2 |
①函数y=f(x)的定义域为R,最大值是
| 1 |
| 2 |
③函数y=f(x)是周期函数,最小正周期为1;④函数y=f(x)的图象的对称中心是(0,0).
其中正确命题的序号是
①③
①③
.分析:本题为新定义问题,因为m为整数,故可取m为几个特殊的整数,作出函数的图象,数形结合进行研究.
解答:解:由题意x-{x}=x-m,
f(x)=|x-{x}|=|x-m|,
m=0时,-
<x≤
,f(x)=|x|,
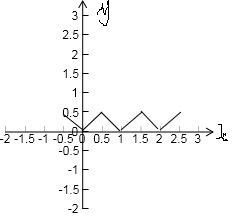
m=1时,1-
<x≤1+
,f(x)=|x-1|,
m=2时,2-
<x≤2+
,f(x)=|x-2|,
由图象可知正确命题为①③,
故答案为:①③.
f(x)=|x-{x}|=|x-m|,
m=0时,-
| 1 |
| 2 |
| 1 |
| 2 |

m=1时,1-
| 1 |
| 2 |
| 1 |
| 2 |
m=2时,2-
| 1 |
| 2 |
| 1 |
| 2 |
由图象可知正确命题为①③,
故答案为:①③.
点评:本题是新定义问题,具有一定难度,容易出错.考查函数的性质,可结合图象进行研究,体现数形结合思想.

练习册系列答案
相关题目