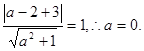题目内容
设直线 与圆
与圆 相交于A、B两点,且弦AB的长为2
相交于A、B两点,且弦AB的长为2 ,则
,则 =________.
=________.
 与圆
与圆 相交于A、B两点,且弦AB的长为2
相交于A、B两点,且弦AB的长为2 ,则
,则 =________.
=________.0
试题分析:当直线与圆相交时,半径、弦长的一半和圆心到弦的距离组成一个直角三角形,所以本题中圆心到直线的距离为
 ,应用点到直线的距离公式有
,应用点到直线的距离公式有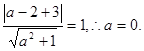
点评:当直线与圆相交时,半径、半弦长和圆心到弦的距离构成一个直角三角形,这个三角形应用十分广泛,要注意灵活应用.

练习册系列答案
相关题目
题目内容
 与圆
与圆 相交于A、B两点,且弦AB的长为2
相交于A、B两点,且弦AB的长为2 ,则
,则 =________.
=________. ,应用点到直线的距离公式有
,应用点到直线的距离公式有