题目内容
15．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x≤0}\\{lo{g}_{4}x，x＞0}\end{array}\right.$，则f[f（-2）]=（ ）| A． | 1 | B． | 2 | C． | -1 | D． | -2 |
分析 利用分段函数逐步求解函数值即可．
解答 解：函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x≤0}\\{lo{g}_{4}x，x＞0}\end{array}\right.$，
则f[f（-2）]=f（2-2）=log42-2=-1．
故选：C．
点评 本题考查分段函数的应用，对数与指数的运算法则的应用，考查计算能力．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
5．下列四组函数中，为同一函数的一组是（ ）
| A． | f（x）=1与g（x）=x0 | B． | f（x）=$\sqrt{x^2}$与g（x）=x | ||
| C． | f（x）=|-x|与g（x）=$\left\{\begin{array}{l}{x}&{x≥0}\\{-x}&{x＜0}\end{array}\right.$ | D． | f（x）=$\frac{{{x^2}-1}}{x-1}$与g（x）=x+1 |
10．下列函数中与函数y=x-1相等的是（ ）
| A． | y=（$\sqrt{x-1}$）2 | B． | y=$\root{3}{（x-1）^{3}}$ | C． | y=$\sqrt{（x-1）^{2}}$ | D． | y=$\frac{（x-1）^{2}}{x-1}$ |
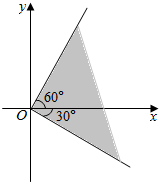已知角α的终边在如图所示的阴影区域内．