题目内容
15.设a=${log}_{\frac{1}{5}}$3,b=($\frac{1}{3}$)0.4,c=4${\;}^{\frac{1}{3}}$,则( )| A. | c>b>a | B. | c>a>b | C. | b>a>c | D. | a>b>c |
分析 利用指数幂对数的运算性质得出a,b,c的范围即可判断大小.
解答 解:根据指数幂,对数函数的性质得出:a=log${\;}_{\frac{1}{5}}$3<0,0<b=($\frac{1}{3}$)0.4<1,c=4${\;}^{\frac{1}{3}}$=$\root{3}{4}$>1,
可以判断出c>b>a
故选:A
点评 本题考查了指数,对数函数的性质,运算,利用中间变量的大小,属于容易题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
5.函数f(x)=ex+lnx在点(1,f(1))处的切线的斜率为( )
| A. | e | B. | e+1 | C. | -1 | D. | 2e |
6.函数f(x)=$\left\{\begin{array}{l}{\frac{ln(x+1)}{x-1}\\;x>1}\\{tan\frac{π}{2}x\\;0≤x<1}\\{x+sinx\\;x<0}\end{array}\right.$的全体连续点的集合是( )
| A. | (-∞,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,1)∪(1,+∞) | D. | (-∞,0)∪(0,1)∪(1,+∞) |
5.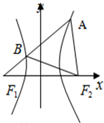 如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )
如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )
 如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )
如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )| A. | 4 | B. | $\sqrt{7}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |