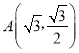题目内容
【题目】设函数
，其中a为常数．
Ⅰ
当
，求a的值；
Ⅱ当
时，关于x的不等式
恒成立，求a的取值范围．
【答案】（1）a=﹣
（2）[﹣2，+∞）
【解析】
（1）直接计算出f（1）和f（2），根据条件解方程即可求得a；
（2）采用分离参数法，分离变量a，再根据函数的单调性求最值，得出a的取值范围．
（1）∵f（x）=log2（1+a2x+4x），
∴f（-1）=log2（1+
+
），f（2）=log2（1+4a+16），
由于
，
即log2（4a+17）=log2（+
）+4，
解得，a=﹣；
（2）因为f（x）≥x﹣1恒成立，
所以，log2（1+a2x+4x）≥x﹣1，
即，1+a2x+4x≥2x﹣1，
分离参数a得，a≥
﹣（2x+2﹣x），
∵x≥1，∴（2x+2﹣x）min=
，此时x=1，
所以，a≥﹣=﹣2，
即实数a的取值范围为[﹣2，+∞）．
练习册系列答案
轻松暑假总复习系列答案
相关题目
【题目】为了解某校学生参加社区服务的情况，采用按性别分层抽样的方法进行调查.已知该校共有学生960人，其中男生560人，从全校学生中抽取了容量为n的样本，得到一周参加社区服务时间的统计数据如下：
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
（1）求m，n；
（2）能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关？
附：
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2
