题目内容
若函数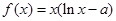 (
( 为实常数).
为实常数).
(1)当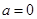 时,求函数
时,求函数 在
在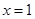 处的切线方程;
处的切线方程;
(2)设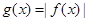 .
.
①求函数 的单调区间;
的单调区间;
②若函数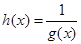 的定义域为
的定义域为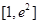 ,求函数
,求函数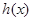 的最小值
的最小值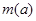 .
.
(1)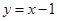 ;(2)①单调增区间为
;(2)①单调增区间为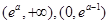 ;单调减区间为
;单调减区间为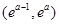 ,②
,②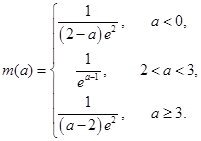
解析试题分析:(1)当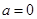 时,
时,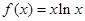 ,先求导,再求出函数在
,先求导,再求出函数在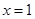 处的导数即所求切线的斜率,就可写出直线的点斜式方程;(2)①分类讨论去掉绝对值,将函数
处的导数即所求切线的斜率,就可写出直线的点斜式方程;(2)①分类讨论去掉绝对值,将函数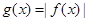 化为分段函数,在不同取值范围内,分别求导判断函数的单调性,②由函数
化为分段函数,在不同取值范围内,分别求导判断函数的单调性,②由函数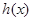 的定义域去判断
的定义域去判断 的取值范围,再结合①的结果,对函数
的取值范围,再结合①的结果,对函数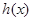 进行分类讨论,分别求出各种情况下的最小值,即得
进行分类讨论,分别求出各种情况下的最小值,即得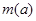 .
.
试题解析:(1)当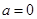 时,
时,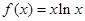 ,
,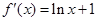 ,
,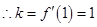 , 2分
, 2分
又当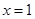 时,
时,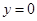 ,
,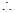 函数
函数 在
在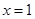 处的切线方程
处的切线方程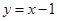 ; 4分
; 4分
(2)因为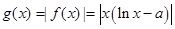
 ,
,
①当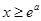 时,
时,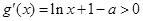 恒成立,所以
恒成立,所以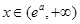 时,函数
时,函数 为增函数; 7分
为增函数; 7分
当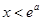 时,
时,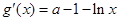 ,令
,令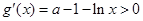 ,得
,得 ,
,
令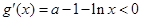 ,得
,得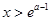 ,
,
所以函数 的单调增区间为
的单调增区间为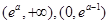 ;单调减区间为
;单调减区间为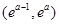 ;10分
;10分
②当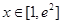 时,
时,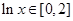 ,因为
,因为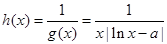 的定义域为
的定义域为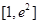 ,以
,以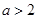 或
或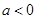 11分(ⅰ)当
11分(ⅰ)当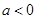 时,
时,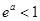 ,所以函数
,所以函数 在
在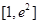 上单调递增,则
上单调递增,则 的最大值为
的最大值为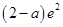 ,
,
所以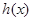 在区间
在区间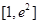 上的最小值为
上的最小值为 ; 13分
; 13分
(ⅱ)当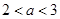 时,
时,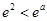 ,且
,且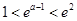 ,所以函数
,所以函数 在
在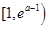 上单调递增,在
上单调递增,在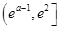 上单调递减,则
上单调递减,则 的最大值为
的最大值为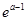 ,所以
,所以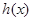 在区间
在区间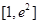 上的最小值为
上的最小值为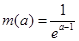 ;14分
;14分
(ⅲ)当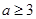 时,
时,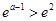 ,所以函数
,所以函数 在
在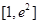 上单调递增,则
上单调递增,则 的最大值为
的最大值为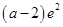 ,所以
,所以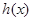 在区间
在区间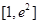 上的最小值为
上的最小值为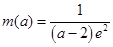 .
.
综上所述,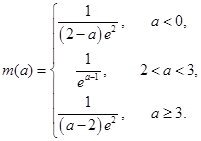 16分
16分
考点:函数的应用、导数的应用.

练习册系列答案
相关题目
 (
( 为常数)的图象过原点,且对任意
为常数)的图象过原点,且对任意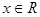 总有
总有 成立;
成立; 的最大值等于1,求
的最大值等于1,求 与
与 的大小关系.
的大小关系.
 在点
在点 处的切线与圆
处的切线与圆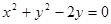 相切,求
相切,求 的值;
的值; 时,函数
时,函数 轴的上方,试求出
轴的上方,试求出 的一个焦点是
的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 .
. 为斜率的直线
为斜率的直线 与双曲线
与双曲线 ,且线段
,且线段 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求 的取值范围.
的取值范围.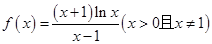 ,
, 的单调性;
的单调性;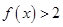 .
. .
. 在
在 上的最小值;
上的最小值; 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,都有
,都有 成立.
成立.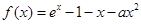 .
.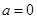 ,求
,求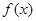 的单调区间;
的单调区间;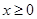 时
时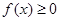 ,求
,求 的取值范围
的取值范围 .
. 时,
时, 单调递增,求
单调递增,求 的取值范围;
的取值范围; 的实数根的个数.
的实数根的个数. .
. 时,求曲线
时,求曲线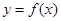 在点
在点 处的切线方程;
处的切线方程; ,且
,且 ,求函数
,求函数 的单调区间.
的单调区间.