题目内容
已知函数 .
.
(1)当 时,求曲线
时,求曲线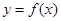 在点
在点 处的切线方程;
处的切线方程;
(2)当 ,且
,且 ,求函数
,求函数 的单调区间.
的单调区间.
(1) 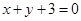 ;(2)当
;(2)当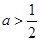 时,
时, 在
在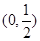 ,
,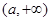 上单调递增,在
上单调递增,在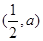 上单调递减,当
上单调递减,当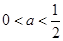 时,
时, 在
在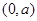 ,
,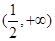 上单调递增,在
上单调递增,在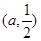 上单调递减.
上单调递减.
解析试题分析:本题综合考查函数与导数及运用导数求单调区间和切线方程等数学知识和方法,考查函数思想、分类讨论思想.第一问,先把 代入,得到
代入,得到 解析式,对它求导,将切点的横坐标代入得到切线的斜率,将1代入到
解析式,对它求导,将切点的横坐标代入得到切线的斜率,将1代入到 表达式中得到切点的纵坐标,最后通过点斜式方程直接写出切线方程;第二问,先对
表达式中得到切点的纵坐标,最后通过点斜式方程直接写出切线方程;第二问,先对 求导,令
求导,令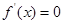 得到方程的2个根
得到方程的2个根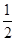 和
和 ,讨论
,讨论 和
和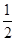 的大小,分情况令
的大小,分情况令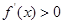 得函数的增区间,
得函数的增区间, 得函数的减区间.
得函数的减区间.
试题解析:(1)当 时,
时,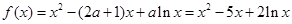 ,
,
∴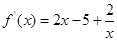 ,(2分)
,(2分)
∴ ,
,
又 ,(4分)
,(4分)
∴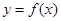 在点
在点 处的切线方程为
处的切线方程为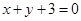 .(5分)
.(5分)
(2)  (
(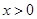 ),
),
令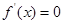 ,可得
,可得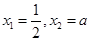 .(6分)
.(6分)
①当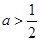 时,由
时,由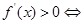
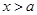 或
或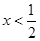 ,
, 在
在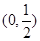 ,
,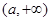 上单调递增.
上单调递增.
由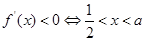 .
. 在
在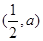 上单调递减.(9分)
上单调递减.(9分)
②当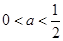 时,由
时,由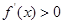 可得
可得 在
在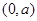 ,
,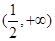 上单调递增.
上单调递增.
由 可得
可得 在
在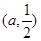 上单调递减.(12分)
上单调递减.(12分)
考点:1.利用导数求切线方程;2.利用导数求函数的单调区间.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
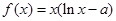 (
( 为实常数).
为实常数).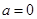 时,求函数
时,求函数 在
在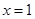 处的切线方程;
处的切线方程;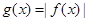 .
. 的单调区间;
的单调区间;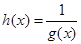 的定义域为
的定义域为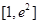 ,求函数
,求函数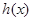 的最小值
的最小值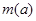 .
. .
. 在
在 上是增函数,求正实数
上是增函数,求正实数 的取值范围;
的取值范围;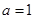 ,
, 且
且 ,设
,设 ,求函数
,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.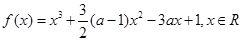 .
. 的单调区间;
的单调区间;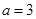 时,若函数
时,若函数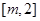 上的最大值为28,求
上的最大值为28,求 的取值范围.
的取值范围.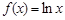 ,
,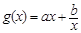 ,函数
,函数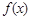 的图象与
的图象与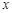 轴的交点也在函数
轴的交点也在函数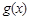 的图象上,且在此点有公切线.
的图象上,且在此点有公切线.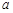 ,
,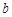 的值;
的值; 与
与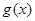 的大小.
的大小.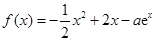 .
.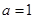 ,求
,求 在
在 处的切线方程;
处的切线方程; 上是增函数,求实数
上是增函数,求实数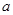 的取值范围.
的取值范围.
 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. 的一个极值点,求
的一个极值点,求 上的最大值.
上的最大值. ,
, .
. 且
且 ,试讨论
,试讨论 的单调性;
的单调性; ,总
,总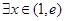 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. -a
-a +x(a>0).
+x(a>0). =
=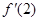 ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程; 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: .
.