题目内容
【题目】设数列![]() 满足:
满足:![]() ,
,![]() (其中
(其中![]() 为非零实常数).
为非零实常数).
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出通项公式;
是等差数列,并求出通项公式;
(2)设![]() ,记
,记![]() ,求使得不等式
,求使得不等式![]() 成立的最小正整数
成立的最小正整数![]() ;
;
(3)若![]() ,对于任意的正整数
,对于任意的正整数![]() ,均有
,均有![]() ,当
,当![]() 、
、![]() 、
、![]() 依次成等比数列时,求
依次成等比数列时,求![]() 、
、![]() 、
、![]() 的值.
的值.
【答案】(1)![]() ,见解析;(2)10;(3)见解析
,见解析;(2)10;(3)见解析
【解析】
(1)![]() 时,根据定义可证数列是等差数列,根据等差数列的通项公式可求;
时,根据定义可证数列是等差数列,根据等差数列的通项公式可求;
(2)![]() 时,将已知变形可得数列
时,将已知变形可得数列![]() 是等比数列,可得
是等比数列,可得![]() 的通项公式,
的通项公式,
可得![]() 的通项公式,再求和解不等式可得;
的通项公式,再求和解不等式可得;
(3)![]() 且
且![]() 时,将已知变形为
时,将已知变形为![]() ,可得数列
,可得数列![]() 为等比数列,可求得
为等比数列,可求得![]() ,再根据数列
,再根据数列![]() 递增可求得
递增可求得![]() ,再由
,再由![]() 、
、![]() 、
、![]() 依次成等比数列,可得
依次成等比数列,可得![]() ,因为
,因为![]() ,所以只能是
,所以只能是![]() .
.
(1)证明:![]() 时,由
时,由![]() 得
得![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,
所以![]() .
.
(2)![]() 时,由
时,由![]() 得
得![]() .
.
因为![]() ,所以数列
,所以数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,
的等比数列,
所以![]()
![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]()
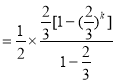
![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]()
![]()
![]() .
.
所以使得不等式![]() 成立的最小正整数
成立的最小正整数![]() 为10.
为10.
(3)![]() 时,由
时,由![]() ,得
,得![]() ,
,
得![]() ,
,
所以![]() ,
,
所以![]() ,
,
由![]() 知
知![]() 为自然数,所以
为自然数,所以![]()
![]() ,
,
又对于任意的正整数![]() ,均有
,均有![]() ,
,
所以数列![]() 为递增数列,
为递增数列,
所以![]() ,又
,又![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() 、
、![]() 、
、![]() 依次成等比数列,
依次成等比数列,
所以![]() ,
,
即![]() .
.
即![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以只能有![]() ,
,
所以![]() ,
,
综上![]() .
.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案【题目】某校抽取了100名学生期中考试的英语和数学成绩,已知成绩都不低于100分,其中英语成绩的频率分布直方图如图所示,成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
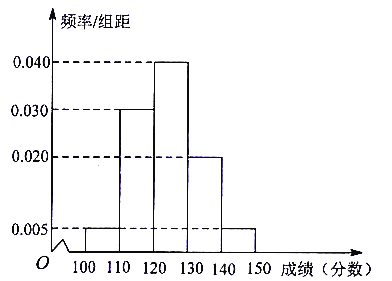
(1)根据频率分布直方图,估计这100名学生英语成绩的平均数和中位数(同一组数据用该区间的中点值作代表);
(2)若这100名学生数学成绩分数段的人数y的情况如下表所示:
分组区间 |
|
|
|
|
|
y | 15 | 40 | 40 | m | n |
且区间![]() 内英语人数与数学人数之比为
内英语人数与数学人数之比为![]() ,现从数学成绩在
,现从数学成绩在![]() 的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在
的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在![]() 的概率.
的概率.
【题目】已知函数![]() .
.
(1)试求函数![]() 的极值点的个数;
的极值点的个数;
(2)若![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
参考数据:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.558 | 2.303 |
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,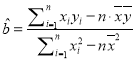 ,
,![]() ,
,![]() .
.
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)用对数回归模型拟合y与x的关系,可得回归方程:![]() ,经计算得出线性回归模型和对数模型的
,经计算得出线性回归模型和对数模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.