Question

已知数列{a_n}满足a₁=31，a_n+1=a_n+2n，n∈N₊，则的最小值是________．

Answer 1

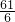
分析：先求出其解析式，进而利用相应函数的导数求其最值即可．
解答：∵数列{a_n}满足a₁=31，a_n+1=a_n+2n，n∈N₊，
∴a_n=（a_n-a_n-1）+（a_n-1-a_n-2）+…+（a₂-a₁）+a₁=2（n-1）+2（n-2）+…+2×1+31=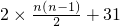=n（n-1）+31．
∴．
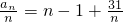设函数f（x）=x+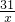-1，（x≥1），则=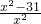，令f^′（x）=0，则，
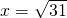∴当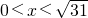时，f^′（x）＜0，即函数f（x）单调递减；当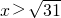时，f^′（x）＞0，即函数f（x）单调递增．
∴当x=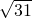时，函数f（x）取得最小值．
根据以上函数f（x）的性质可知：对于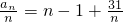来说，当n=6时，此式取得最小值．
故答案为．
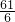点评：正确求出解析式和转化利用函数的单调性求最值是解题的关键．