题目内容
设函数
 ,其中
,其中 ,
,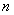 为正整数,
为正整数,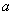 、
、 、
、 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
.
(1)求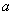 、
、 、
、 的值;
的值;
(2)求函数 的最大值;
的最大值;
(3)证明:对任意的 都有
都有 .(
.(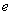 为自然对数的底)
为自然对数的底)
【答案】
(1) ,
, ,
, ;(2)
;(2) ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)利用点 在切线
在切线 上,求出
上,求出 的值,由切线方程求出切线的斜率,从而得到
的值,由切线方程求出切线的斜率,从而得到 的值,再结合题干的条件列方程组求出
的值,再结合题干的条件列方程组求出 、
、 、
、 的值;(2)利用导数求出极值,利用极值与最值的关系求出最大值;(3)证法1是利用分析法将问题
的值;(2)利用导数求出极值,利用极值与最值的关系求出最大值;(3)证法1是利用分析法将问题 等价转化为证明不等式
等价转化为证明不等式 ,最后等价证明
,最后等价证明 ,利用换元法
,利用换元法 ,构造新函数
,构造新函数 ,只需证明不等式
,只需证明不等式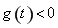 即可,利用导数,结合单调性进行证明;证法2是先构造新函数
即可,利用导数,结合单调性进行证明;证法2是先构造新函数 ,证明
,证明 在区间内成立,再令
在区间内成立,再令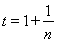 ,得到
,得到 ,最终得到
,最终得到 ,再结合(2)中的结论得到
,再结合(2)中的结论得到 .
.
试题解析:(1) 由点
由点 在直线
在直线 上,可得
上,可得 ,即
,即 .
.
 ,
, .
.
又 切线
切线 的斜率为
的斜率为 ,
, ,
, ,
, ,
, ;
;
(2)由(1)知, ,故
,故 .
.
令 ,解得
,解得 ,即
,即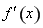 在
在 上有唯一零点
上有唯一零点 .
.
当 时,
时,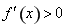 ,故
,故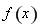 在
在 上单调递增;
上单调递增;
当 时,
时, ,故
,故 在
在 单调递减.
单调递减.
 在
在 上的最大值
上的最大值 .
.
(3)证法1:要证对任意的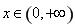 都有
都有 ,只需证
,只需证 ,
,
由(2)知在 上
上 有最大值,
有最大值, ,故只需证
,故只需证 .
.
即 ,即
,即 ,①
,①
令 ,则
,则 ,①即
,①即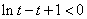 ,②
,②
令 ,则
,则 ,
,
显然当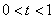 时,
时, ,所以
,所以 在
在 上单调递增,
上单调递增,
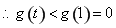 ,即对任意的
,即对任意的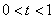 ②恒成立,
②恒成立,
 对任意的
对任意的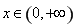 都有
都有 ;
;
证法2:令 ,则
,则 .
.
当 时,
时, ,故
,故 在
在 上单调递减;
上单调递减;
而当 时,
时,  ,故
,故 在
在 上单调递增.
上单调递增.
 在
在 上有最小值,
上有最小值,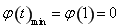 .
.
 ,即
,即 .
.
令 ,得
,得 ,即
,即 ,所以
,所以 ,即
,即 .
.
由(2)知, ,故所证不等式成立.
,故所证不等式成立.
考点:1.利用导数求切线方程;2.利用导数求函数的最值;3.函数不等式

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 ,其中
,其中 是函数
是函数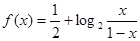 图象上任意两点,且
图象上任意两点,且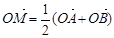 ,已知点
,已知点 的横坐标为
的横坐标为 ,且有
,且有 ,其中
,其中 且n≥2,
且n≥2, ,
, ,
, 及
及 ;
;  ,其中
,其中 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 +log2
+log2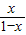 图象上任意两点,且
图象上任意两点,且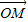 =
= (
(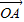 +
+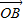 ),已知点M的横坐标为
),已知点M的横坐标为 ,且有Sn=f(
,且有Sn=f(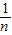 )+f(
)+f(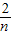 )+…+f(
)+…+f(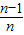 ),其中n∈N*且n≥2,
),其中n∈N*且n≥2,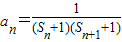 ,其中n∈N*,且Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.
,其中n∈N*,且Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.