题目内容
设A(x1,y1),B(x2,y2)是函数f(x)= +log2
+log2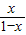 图象上任意两点,且
图象上任意两点,且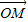 =
= (
(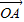 +
+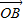 ),已知点M的横坐标为
),已知点M的横坐标为 ,且有Sn=f(
,且有Sn=f(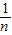 )+f(
)+f(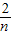 )+…+f(
)+…+f(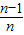 ),其中n∈N*且n≥2,
),其中n∈N*且n≥2,(1)求点M的纵坐标值;
(2)求s2,s3,s4及Sn;
(3)已知
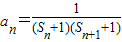 ,其中n∈N*,且Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.
,其中n∈N*,且Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.
【答案】分析:(1)由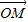 =
= (
(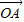 +
+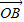 )知M为线段AB的中点,由M的横坐标为
)知M为线段AB的中点,由M的横坐标为 得x1+x2=1,由此可求得y1+y2,从而可得点M的纵坐标;
得x1+x2=1,由此可求得y1+y2,从而可得点M的纵坐标;
(2)根据Sn=f(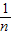 )+f(
)+f(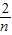 )+…+f(
)+…+f(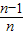 ),分别令n=2,3,4即可求得s2,s3,s4;由(1)知,由
),分别令n=2,3,4即可求得s2,s3,s4;由(1)知,由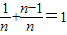 ,得f(
,得f(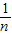 )+f(
)+f(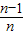 )=1,从而可求得2Sn;
)=1,从而可求得2Sn;
(3)先表示出an,利用裂项相消法求得Tn,分离出参数λ后转化为求函数的最值可解决,利用基本不等式可得最值;
解答:解:(1)依题意,由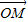 =
= (
(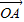 +
+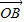 )知M为线段AB的中点,
)知M为线段AB的中点,
又因为M的横坐标为 ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),
∴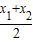 =
= ,即x1+x2=1,
,即x1+x2=1,
∴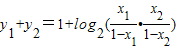 =1+log21=1,
=1+log21=1,
所以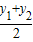 =
= ,
,
即点M的横坐标为定值 ;
;
(2)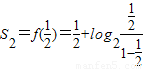 =
= ,
,
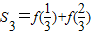 =
=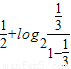 +
+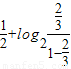 =1,
=1,
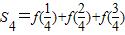 =
=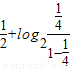 +
+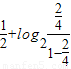 +
+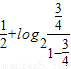 =
= ,
,
由(1)知,由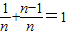 ,得f(
,得f(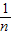 )+f(
)+f(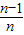 )=1,
)=1,
又Sn=f(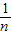 )+f(
)+f(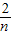 )+…+f(
)+…+f(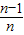 )=f(
)=f(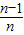 )+f(
)+f(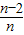 )+…+f(
)+…+f(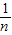 ),
),
所以2Sn=(n-1)×1,即Sn=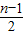 (n∈N*且n≥2);
(n∈N*且n≥2);
(3)当n≥2时,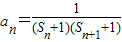 =
=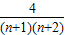 ,
,
又n=1时,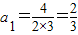 也适合,
也适合,
所以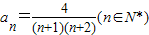 ,
,
∴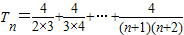 =4(
=4(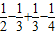
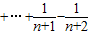 )
)
=4(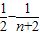 )=
)=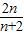 (n∈N*),
(n∈N*),
由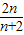 ≤λ
≤λ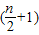 恒成立(n∈N*)推得λ≥
恒成立(n∈N*)推得λ≥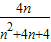 ,
,
而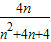 =
=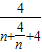
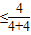 =
= (当且仅当n=2取等号),
(当且仅当n=2取等号),
∴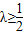 ,∴λ的最小正整数为1.
,∴λ的最小正整数为1.
点评:本题考查数列与不等式、数列与向量的综合,考查恒成立问题,考查转化思想,综合性强,难度较大.
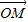 =
= (
(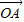 +
+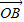 )知M为线段AB的中点,由M的横坐标为
)知M为线段AB的中点,由M的横坐标为 得x1+x2=1,由此可求得y1+y2,从而可得点M的纵坐标;
得x1+x2=1,由此可求得y1+y2,从而可得点M的纵坐标;(2)根据Sn=f(
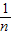 )+f(
)+f(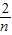 )+…+f(
)+…+f(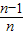 ),分别令n=2,3,4即可求得s2,s3,s4;由(1)知,由
),分别令n=2,3,4即可求得s2,s3,s4;由(1)知,由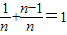 ,得f(
,得f(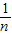 )+f(
)+f(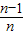 )=1,从而可求得2Sn;
)=1,从而可求得2Sn;(3)先表示出an,利用裂项相消法求得Tn,分离出参数λ后转化为求函数的最值可解决,利用基本不等式可得最值;
解答:解:(1)依题意,由
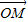 =
= (
(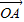 +
+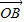 )知M为线段AB的中点,
)知M为线段AB的中点,又因为M的横坐标为
 ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),∴
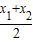 =
= ,即x1+x2=1,
,即x1+x2=1,∴
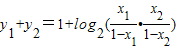 =1+log21=1,
=1+log21=1,所以
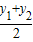 =
= ,
,即点M的横坐标为定值
 ;
;(2)
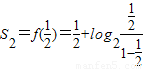 =
= ,
,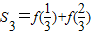 =
=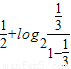 +
+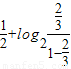 =1,
=1,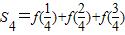 =
=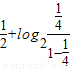 +
+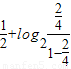 +
+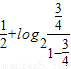 =
= ,
,由(1)知,由
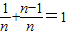 ,得f(
,得f(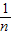 )+f(
)+f(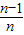 )=1,
)=1,又Sn=f(
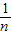 )+f(
)+f(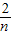 )+…+f(
)+…+f(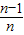 )=f(
)=f(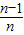 )+f(
)+f(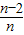 )+…+f(
)+…+f(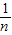 ),
),所以2Sn=(n-1)×1,即Sn=
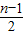 (n∈N*且n≥2);
(n∈N*且n≥2);(3)当n≥2时,
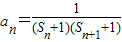 =
=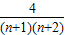 ,
,又n=1时,
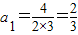 也适合,
也适合,所以
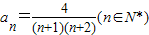 ,
,∴
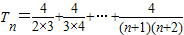 =4(
=4(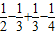
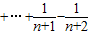 )
)=4(
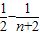 )=
)=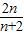 (n∈N*),
(n∈N*),由
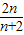 ≤λ
≤λ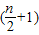 恒成立(n∈N*)推得λ≥
恒成立(n∈N*)推得λ≥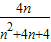 ,
,而
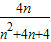 =
=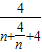
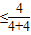 =
= (当且仅当n=2取等号),
(当且仅当n=2取等号),∴
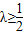 ,∴λ的最小正整数为1.
,∴λ的最小正整数为1.点评:本题考查数列与不等式、数列与向量的综合,考查恒成立问题,考查转化思想,综合性强,难度较大.

练习册系列答案
相关题目
