题目内容
【题目】阅读：
已知
、
，
，求
的最小值.
解法如下：
，
当且仅当
，即
时取到等号，
则的最小值为
.
应用上述解法，求解下列问题：
（1）已知
，
，求
的最小值；
（2）已知
，求函数
的最小值；
（3）已知正数
、
、
，
，
求证：
.
【答案】（1）9；（2）18；（3）证明见解析.
【解析】
试题分析：本题关键是阅读给定的材料，弄懂弄清给定材料提供的方法（“1”的代换），并加以运用.主要就是
，展开后就可应用基本不等式求得最值.（1）
；（2）虽然没有已知的“1”，但观察求值式子的分母，可以凑配出“1”：
，因此有
，展开后即可应用基本不等式；（3）观察求证式的分母，结合已知有
，因此有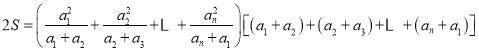
此式中关键是凑配出基本不等式所需要的两项，如
与
合并相加利用基本不等式有
，从而最终得出
.
（1）
，
2分
而
，
当且仅当
时取到等号，则
，即
的最小值为
. 5分
（2）
， 7分
而
，
，
当且仅当
，即
时取到等号，则
，
所以函数
的最小值为
. 10分
（3）
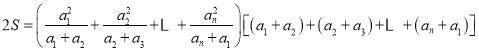
当且仅当
时取到等号，则
. 16分
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】已知随机变量
的取值为不大于
的非负整数值，它的分布列为：
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中
（
）满足： 
，且
．
定义由
生成的函数
，令
．
（I）若由
生成的函数
，求
的值；
（II）求证：随机变量
的数学期望
， 
的方差
；
（
）
（Ⅲ）现投掷一枚骰子两次，随机变量
表示两次掷出的点数之和，此时由
生成的函数记为
，求
的值．
