题目内容
求函数y=(sinx+1)(cosx+1)x∈[0,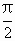 ]的最值,并求相应的x的值.
]的最值,并求相应的x的值.
答案:
解析:
解析:
|
解:因为y=sinxcosx+sinx+cosx+1 x∈[0, |

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
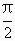 ],令sinx+cosx=t,则sinxcosx=
],令sinx+cosx=t,则sinxcosx=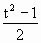 .因为t=sinx+cosx=
.因为t=sinx+cosx=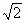 sin(x+
sin(x+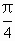 ),而
),而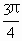 .所以
.所以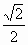 ≤sin(x+
≤sin(x+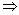 1≤t≤
1≤t≤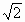 .所以y=
.所以y=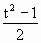 +t+1=
+t+1=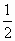 (t2+2t+1)=
(t2+2t+1)=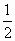 (t+1)2.显然,当t=1时,即
(t+1)2.显然,当t=1时,即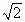 sin(x+
sin(x+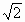 时,即x=
时,即x=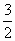 +
+ .
.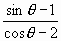 的最大值和最小值.
的最大值和最小值.