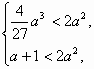题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解:由已知
所求,所求切线斜率为 切线方程为 所以,函数y=f(x)过点P的切线过点(b,0)…………4分 |
(2) |
解:因为
当 在 所以,根据题意有 解之得 当 所以,根据题意有 即 令
综上可知: |

练习册系列答案
相关题目
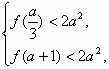 即
即