题目内容
解答题
求函数y=|3x-x3|在[-2,2]上的最大值.
答案:
解析:
解析:
|
解:∵y=f(x)是偶函数,故只要考察[0,2]的最大值即可 f(x)= f′(x)= 令f′(x)=0,x1=1,x2= 故f(x)在[0,2]上的最大值为2,故此函数的最大值为2.12分 |

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
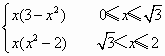 (3分)
(3分)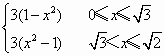 (6分)
(6分)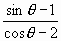 的最大值和最小值.
的最大值和最小值.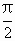 ]的最值,并求相应的x的值.
]的最值,并求相应的x的值.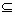 D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.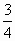 x+
x+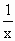 (x∈R+)是否为闭函数?并说明理由;
(x∈R+)是否为闭函数?并说明理由;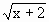 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.