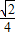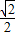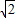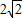题目内容
已知角A、B为锐角,且cos(A+B)•sinB=sinA,则tanA的最大值是( )
分析:由条件可得-cosCsinB=sinA,利用正弦定理和余弦定理可得3a2+b2=c2,由 tan2A=
-1,且A为锐角,判断知,
求tanA的最大值即求cosA的最小值,由基本不等式求出cosA的最小值,从而求得tanA的最大值.
| 1 |
| cos2A |
求tanA的最大值即求cosA的最小值,由基本不等式求出cosA的最小值,从而求得tanA的最大值.
解答:解:由cos(A+B)sinB=sinA得-cosCsinB=sinA,
利用正弦定理和余弦定理,-
×b=a,化简可得 3a2+b2=c2.
由 tan2A=
-1,且A为锐角可得,可得 cosA>0,tanA>0.
只要求出cosA的最小值,就可求得tanA的最大值.
又cosA=
=
≥
,当且仅当
b=c时,等号成立.
即cosA的最小值为
. 故tan2A 的最大值为
,
故tanA的最大值
=
.
利用正弦定理和余弦定理,-
| a2+b2-c2 |
| 2ab |
由 tan2A=
| 1 |
| cos2A |
只要求出cosA的最小值,就可求得tanA的最大值.
又cosA=
| b2+c2-a2 |
| 2bc |
| 2b2+c2 |
| 3bc |
2
| ||
| 3 |
| 2 |
即cosA的最小值为
2
| ||
| 3 |
| 1 |
| 8 |
故tanA的最大值
|
| ||
| 4 |
点评:本题主要考查三角函数的恒等变换及化简求值,正弦定理和余弦定理、基本不等式的应用,属于中档题.

练习册系列答案
相关题目