题目内容
在△ABC中,a,b,c分别为三个内角A,B,C所对的边,设向量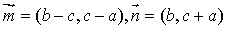 ,若
,若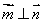 ,则角A的大小为( )
,则角A的大小为( )
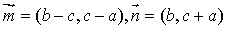 ,若
,若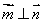 ,则角A的大小为( )
,则角A的大小为( )A.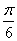 | B.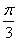 | C.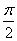 | D.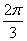 |
B
试题分析:因为,向量
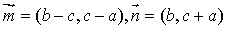 ,且
,且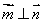 ,
,所以,
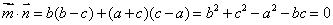 ,
,由余弦定理得,
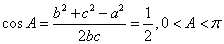 ,故,角A的大小为
,故,角A的大小为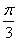 ,选B。
,选B。点评:小综合题,两向量垂直,它们的数量积为0.三角形中求角问题,一般的利用余弦定理。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
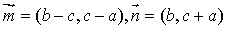 ,若
,若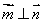 ,则角A的大小为( )
,则角A的大小为( )A.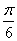 | B.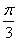 | C.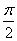 | D.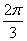 |
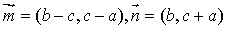 ,且
,且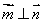 ,
,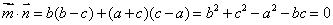 ,
,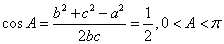 ,故,角A的大小为
,故,角A的大小为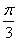 ,选B。
,选B。
 名校课堂系列答案
名校课堂系列答案