题目内容
【题目】选修4-5:不等式选讲
已知![]() ,且
,且![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)求![]() 的最大值.
的最大值.
【答案】(1)8;(2)![]() .
.
【解析】试题分析: (Ⅰ)根据题中等式由基本不等式放缩,可得![]() 的范围,再由
的范围,再由![]() 可得最小值; (Ⅱ)结合要求的最值可得
可得最小值; (Ⅱ)结合要求的最值可得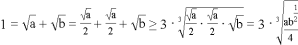 ,所以
,所以![]() ,验证取等条件求出最值.
,验证取等条件求出最值.
试题解析:(Ⅰ)由![]() ,可得
,可得![]() ,
,
![]() ,
,
当且仅当![]() 时等号成立,因此
时等号成立,因此![]() 的最小值为8.
的最小值为8.
(Ⅱ)因为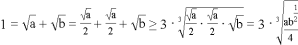 ,
,
所以![]() ,
,
当且仅当![]() ,即
,即![]() 且
且![]() 时,等号成立.
时,等号成立.
点睛:本题考查学生利用基本不等式与和或者乘积的定值求最值的问题,属于中档题目. 解此类题目的两个技巧: (1)创设运用基本不等式的条件,合理拆分项或配凑因式,其目的在于使等号能够成立.(2)既要记住基本不等式的原始形式,而且还要掌握它的变形形式及公式的逆用等,例如:ab≤![]() 2≤
2≤![]() ,
,![]() ≤
≤![]() ≤
≤ ![]() (a>0,b>0).
(a>0,b>0).

【题目】据报道,巴基斯坦由中方投资运营的瓜达尔港目前已通航.这是一个可以停靠8![]() 10万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约340亿美元,公路投资约59亿美元,铁路投资约38亿美元,高架铁路投资约16亿美元,瓜达尔港投资约6.6亿美元,光纤通讯投资约为0.4亿美元.
10万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约340亿美元,公路投资约59亿美元,铁路投资约38亿美元,高架铁路投资约16亿美元,瓜达尔港投资约6.6亿美元,光纤通讯投资约为0.4亿美元.
有消息称,瓜达尔港的月货物吞吐量将是目前天津、上海两港口月货物吞吐量之和.表格记录了2015年天津、上海两港口的月吞吐量(单位:百万吨):
1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
天津 | 24 | 22 | 26 | 23 | 24 | 26 | 27 | 25 | 28 | 24 | 25 | 26 |
上海 | 32 | 27 | 33 | 31 | 30 | 31 | 32 | 33 | 30 | 32 | 30 | 30 |
(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;
(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;
(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设![]() 为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出
为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出![]() 的数学期望(不需要计算过程).
的数学期望(不需要计算过程).