题目内容
【题目】若奇函数y=f(x)在区间(0,+∞)上是增函数,又f(﹣3)=0,则不等式f(x)<0的解集为( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(0,3)
D.(﹣∞,﹣3)∪(3,+∞)
【答案】C
【解析】解:∵f(x)是奇函数,f(﹣3)=0, ∴f(﹣3)=﹣f(3)=0,解f(3)=0.
∵函数在(0,+∞)内是增函数,
∴当0<x<3时,f(x)<0.
当x>3时,f(x)>0,
∵函数f(x)是奇函数,
∴当﹣3<x<0时,f(x)>0.
当x<﹣3时,f(x)<0,
则不等式f(x)<0的解集{x|x<﹣3或0<x<3}.
故选C.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)计算回归系数 ![]() ,
, ![]() .公式为
.公式为 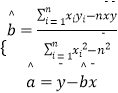 .
.