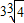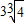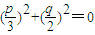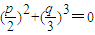Question

若曲线y=x³+px+q与x轴相切，则p，q之间的关系满足（　　）

• A、(

  p

  3

  )2+(

  q

  2

  )2=0
• B、(

  p

  2

  )2+(

  q

  3

  )3=0
• C、2p-3q²=0
• D、2q-3p²=0

Answer 1

分析：求函数的导数，令其为0，求出切点坐标，代入曲线方程得p，q之间的关系．

解答：解：y′=3x²+p
令y′=3x²+p=0得x=

- p 3

或-

- p 3

∵y=0是切线
∴切点为（

- p 3

，0）或（-

- p 3

，0）
代入曲线y=x³+px+q得
(

p

3

)3+(

q

2

)2=0
故选项为B

点评：考查导数在切点处的值为切线的斜率；切点在切线上又在曲线上．