题目内容
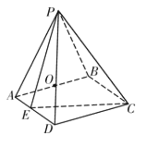
【题目】已知四棱锥![]() 中,面
中,面![]() 面
面![]() ,底面
,底面![]() 为矩形,且
为矩形,且![]() ,
,![]() ,
,![]() ,O为
,O为![]() 的中点,点E在
的中点,点E在![]() 上,且
上,且![]() .
.
(1)证明:![]() ;
;
(2)在![]() 上是否存在一点F,使
上是否存在一点F,使![]() 面
面![]() ,若存在,试确定点F的位置.
,若存在,试确定点F的位置.
【答案】(1)证明见解析(2)存在F为PB的三等分点(靠近点B),证明见解析
【解析】
(1)连接![]() ,利用勾股定理可证明
,利用勾股定理可证明![]() ,由面
,由面![]() 面
面![]() 可得
可得![]() ,可得
,可得![]() 面
面![]() ,即可求证;
,即可求证;
(2)取F为PB的三等分点(靠近点B),N为BC的三等分点(靠近点B ),连接![]() ,可证明平面
,可证明平面![]() 平面
平面![]() ,即可得证
,即可得证
(1)连接![]() ,
,![]() ,如图,
,如图,
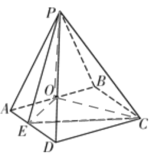
在四棱锥![]() 中,
中,![]() ,O为
,O为![]() 的中点,
的中点,
![]() ,又面
,又面![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
![]()
在矩形![]() 中,
中,![]() ,
,![]() ,
,![]()
由勾股定理知![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
又![]() ,
,
![]() 面
面![]() ,又
,又![]() 平面
平面![]() ,
,
![]()
(2)存在F为PB的三等分点(靠近点B).
证明:取BC的三等分点M (靠近点C ) ,连接AM , 如图
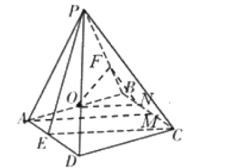
易知![]() ,
,![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
取BM中点N,连接ON,
![]()
![]()
![]() N为BM中点,
N为BM中点,![]() N为BC的三等分点(靠近点B ),
N为BC的三等分点(靠近点B ),
连接![]() ,
,
![]() ,
,
又![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]()
![]()
![]() 面
面![]()

【题目】某购物商场分别推出支付宝和微信“扫码支付”购物活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用“扫码支付”.现统计了活动刚推出一周内每天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次,统计数据如下表所示:
表示每天使用扫码支付的人次,统计数据如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据散点图判断,在推广期内,扫码支付的人![]() 次关于活动推出天数
次关于活动推出天数![]() 的回归方程适合用
的回归方程适合用![]() 来表示,求出该回归方程,并预测活动推出第
来表示,求出该回归方程,并预测活动推出第![]() 天使用扫码支付的人次;
天使用扫码支付的人次;
(2)推广期结束后,商场对顾客的支付方式进行统计,结果如下表:
支付方式 | 现金 | 会员卡 | 扫码 |
比例 |
|
|
|
商场规定:使用现金支付的顾客无优惠,使用会员卡支付的顾客享受![]() 折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受
折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() .现有一名顾客购买了
.现有一名顾客购买了![]() 元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
参考数据:设![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: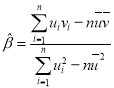 ,
,![]() .
.
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .以原点为极点,
.以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() ,求
,求![]() .
.
【题目】![]() 年是打赢蓝天保卫战三年行动计划的決胜之年,近年来,在各地各部门共同努力下,蓝天保卫战各项任务措施稳步推进,取得了积极成效,某学生随机收集了甲城市近两年上半年中各
年是打赢蓝天保卫战三年行动计划的決胜之年,近年来,在各地各部门共同努力下,蓝天保卫战各项任务措施稳步推进,取得了积极成效,某学生随机收集了甲城市近两年上半年中各![]() 天的空气量指数
天的空气量指数![]() ,得到频数分布表如下:
,得到频数分布表如下:
![]() 年上半年中
年上半年中![]() 天的
天的![]() 频数分布表
频数分布表
|
|
|
|
|
|
天数 |
|
|
|
|
|
![]() 年上半年中
年上半年中![]() 天的
天的![]() 频数分布表
频数分布表
|
|
|
|
|
|
天数 |
|
|
|
|
|
(1)估计![]() 年上半年甲城市空气质量优良天数的比例;
年上半年甲城市空气质量优良天数的比例;
(2)求![]() 年上半年甲城市
年上半年甲城市![]() 的平均数和标准差的估计值(同一组中的数据用该组区间的中点值为代表);(精确到
的平均数和标准差的估计值(同一组中的数据用该组区间的中点值为代表);(精确到![]() )
)
(3)用所学的統计知识,比较![]() 年上半年与
年上半年与![]() 年上半年甲城市的空气质量情况.
年上半年甲城市的空气质量情况.
附:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
![]() .
.