ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΙΚΈο…Χ≥ΓΖ÷±πΆΤ≥ω÷ßΗΕ±ΠΚΆΈΔ–≈ΓΑ…®¬κ÷ßΗΕΓ±ΙΚΈοΜνΕ·Θ§ΜνΕ·…η÷ΟΝΥ“ΜΕΈ ±ΦδΒΡΆΤΙψΤΎΘ§”…”ΎΆΤΙψΤΎΡΎ”≈ΜίΝΠΕ»Ϋœ¥σΘ§Έϋ“ΐ‘Ϋά¥‘ΫΕύΒΡ»ΥΩΣ Φ Ι”ΟΓΑ…®¬κ÷ßΗΕΓ±Θ°œ÷Ά≥ΦΤΝΥΜνΕ·Η’ΆΤ≥ω“Μ÷ήΡΎΟΩΧλ Ι”Ο…®¬κ÷ßΗΕΒΡ»Υ¥ΈΘ§”Ο![]() ±μ ΨΜνΕ·ΆΤ≥ωΒΡΧλ ΐΘ§
±μ ΨΜνΕ·ΆΤ≥ωΒΡΧλ ΐΘ§![]() ±μ ΨΟΩΧλ Ι”Ο…®¬κ÷ßΗΕΒΡ»Υ¥ΈΘ§Ά≥ΦΤ ΐΨί»γœ¬±μΥυ ΨΘΚ
±μ ΨΟΩΧλ Ι”Ο…®¬κ÷ßΗΕΒΡ»Υ¥ΈΘ§Ά≥ΦΤ ΐΨί»γœ¬±μΥυ ΨΘΚ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
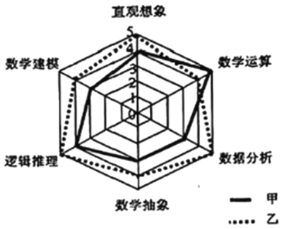
Θ®1Θ©ΗυΨί…ΔΒψΆΦ≈–ΕœΘ§‘ΎΆΤΙψΤΎΡΎΘ§…®¬κ÷ßΗΕΒΡ»Υ![]() ¥ΈΙΊ”ΎΜνΕ·ΆΤ≥ωΧλ ΐ
¥ΈΙΊ”ΎΜνΕ·ΆΤ≥ωΧλ ΐ![]() ΒΡΜΊΙιΖΫ≥Χ Κœ”Ο
ΒΡΜΊΙιΖΫ≥Χ Κœ”Ο![]() ά¥±μ ΨΘ§«σ≥ωΗΟΜΊΙιΖΫ≥ΧΘ§≤Δ‘Λ≤βΜνΕ·ΆΤ≥ωΒΎ
ά¥±μ ΨΘ§«σ≥ωΗΟΜΊΙιΖΫ≥ΧΘ§≤Δ‘Λ≤βΜνΕ·ΆΤ≥ωΒΎ![]() Χλ Ι”Ο…®¬κ÷ßΗΕΒΡ»Υ¥ΈΘΜ
Χλ Ι”Ο…®¬κ÷ßΗΕΒΡ»Υ¥ΈΘΜ
Θ®2Θ©ΆΤΙψΤΎΫα χΚσΘ§…Χ≥ΓΕ‘ΙΥΩΆΒΡ÷ßΗΕΖΫ ΫΫχ––Ά≥ΦΤΘ§ΫαΙϊ»γœ¬±μΘΚ
÷ßΗΕΖΫ Ϋ | œ÷Ϋπ | Μα‘±Ω® | …®¬κ |
±»άΐ |
|
|
|
…Χ≥ΓΙφΕ®ΘΚ Ι”Οœ÷Ϋπ÷ßΗΕΒΡΙΥΩΆΈό”≈ΜίΘ§ Ι”ΟΜα‘±Ω®÷ßΗΕΒΡΙΥΩΆœμ ή![]() ’έ”≈ΜίΘ§…®¬κ÷ßΗΕΒΡΙΥΩΆΥφΜζ”≈ΜίΘ§ΗυΨίΆ≥ΦΤΫαΙϊΒΟ÷ΣΘ§ Ι”Ο…®¬κ÷ßΗΕΒΡΙΥΩΆΘ§œμ ή
’έ”≈ΜίΘ§…®¬κ÷ßΗΕΒΡΙΥΩΆΥφΜζ”≈ΜίΘ§ΗυΨίΆ≥ΦΤΫαΙϊΒΟ÷ΣΘ§ Ι”Ο…®¬κ÷ßΗΕΒΡΙΥΩΆΘ§œμ ή![]() ’έ”≈ΜίΒΡΗ≈¬ ΈΣ
’έ”≈ΜίΒΡΗ≈¬ ΈΣ![]() Θ§œμ ή
Θ§œμ ή![]() ’έ”≈ΜίΒΡΗ≈¬ ΈΣ
’έ”≈ΜίΒΡΗ≈¬ ΈΣ![]() Θ§œμ ή
Θ§œμ ή![]() ’έ”≈ΜίΒΡΗ≈¬ ΈΣ
’έ”≈ΜίΒΡΗ≈¬ ΈΣ![]() Θ°œ÷”–“ΜΟϊΙΥΩΆΙΚ¬ρΝΥ
Θ°œ÷”–“ΜΟϊΙΥΩΆΙΚ¬ρΝΥ![]() ‘ΣΒΡ…ΧΤΖΘ§ΗυΨίΥυΗχ ΐΨί”Ο ¬ΦΰΖΔ…ζΒΡΤΒ¬ ά¥ΙάΦΤœύ”Π ¬ΦΰΖΔ…ζΒΡΗ≈¬ Θ§ΙάΦΤΗΟΙΥΩΆ÷ßΗΕΒΡΤΫΨυΖ―”Ο «Εύ…ΌΘΩ
‘ΣΒΡ…ΧΤΖΘ§ΗυΨίΥυΗχ ΐΨί”Ο ¬ΦΰΖΔ…ζΒΡΤΒ¬ ά¥ΙάΦΤœύ”Π ¬ΦΰΖΔ…ζΒΡΗ≈¬ Θ§ΙάΦΤΗΟΙΥΩΆ÷ßΗΕΒΡΤΫΨυΖ―”Ο «Εύ…ΌΘΩ
≤ΈΩΦ ΐΨίΘΚ…η![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]()
≤ΈΩΦΙΪ ΫΘΚΕ‘”Ύ“ΜΉι ΐΨί![]() Θ§
Θ§![]() Θ§Γ≠Θ§
Θ§Γ≠Θ§![]() Θ§ΤδΜΊΙι÷±œΏ
Θ§ΤδΜΊΙι÷±œΏ![]() ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ
ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ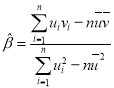 Θ§
Θ§![]() Θ°
Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΜΊΙιΖΫ≥ΧΈΣΘΚ![]() ΘΜΜνΕ·ΆΤ≥ωΒΎ8Χλ Ι”Ο…®¬κ÷ßΗΕΒΡ»Υ¥ΈΈΣ331Θ®2Θ©“ΜΟϊΙΥΩΆΙΚΈοΒΡΤΫΨυΖ―”ΟΈΣ
ΘΜΜνΕ·ΆΤ≥ωΒΎ8Χλ Ι”Ο…®¬κ÷ßΗΕΒΡ»Υ¥ΈΈΣ331Θ®2Θ©“ΜΟϊΙΥΩΆΙΚΈοΒΡΤΫΨυΖ―”ΟΈΣ![]() ‘Σ
‘Σ
ΓΨΫβΈωΓΩ
Θ®1Θ©”…![]() Θ§ΝΫ±ΏΆ§ ±»Γ≥Θ”ΟΕ‘ ΐΒΟΘΚ
Θ§ΝΫ±ΏΆ§ ±»Γ≥Θ”ΟΕ‘ ΐΒΟΘΚ![]() ΘΜ…η
ΘΜ…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§άϊ”ΟΉν–ΓΕΰ≥ΥΖ®«σ≥ω
Θ§άϊ”ΟΉν–ΓΕΰ≥ΥΖ®«σ≥ω![]() Θ§ΫχΕχ«σΒΟΜΊΙιΖΫ≥ΧΘΜ‘ΌΫΪ
Θ§ΫχΕχ«σΒΟΜΊΙιΖΫ≥ΧΘΜ‘ΌΫΪ![]() ¥ζ»κΖΫ≥ΧΫχ––‘Λ±®÷Β«σΫβΘΜ
¥ζ»κΖΫ≥ΧΫχ––‘Λ±®÷Β«σΫβΘΜ
Θ®2Θ©Φ«“ΜΟϊΙΥΩΆΙΚΈο÷ßΗΕΒΡΖ―”ΟΈΣ![]() Θ§–¥≥ω
Θ§–¥≥ω![]() ΒΡΥυ”–Ω…Ρή»Γ÷ΒΚΆΥφΜζ±δΝΩΒΡΖ÷≤ΦΝ–Θ§¥”Εχ«σΒΟΙΥΩΆ÷ßΗΕΒΡΤΫΨυΖ―”Ο.
ΒΡΥυ”–Ω…Ρή»Γ÷ΒΚΆΥφΜζ±δΝΩΒΡΖ÷≤ΦΝ–Θ§¥”Εχ«σΒΟΙΥΩΆ÷ßΗΕΒΡΤΫΨυΖ―”Ο.
Θ®1Θ©”…![]() Θ§ΝΫ±ΏΆ§ ±»Γ≥Θ”ΟΕ‘ ΐΒΟΘΚ
Θ§ΝΫ±ΏΆ§ ±»Γ≥Θ”ΟΕ‘ ΐΒΟΘΚ![]() ΘΜ
ΘΜ
…η![]()
![]()
![]() Θ§
Θ§![]() Θ§
Θ§
 Θ§
Θ§
Α――υ±Ψ÷––ΡΒψ![]() ¥ζ»κ
¥ζ»κ![]() ,ΒΟ:
,ΒΟ:![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙιΖΫ≥ΧΈΣΘΚ
ΒΡΜΊΙιΖΫ≥ΧΈΣΘΚ![]() ΘΜ
ΘΜ
Α―![]() ¥ζ»κ…œ ΫΘ§
¥ζ»κ…œ ΫΘ§![]() ΘΜ
ΘΜ
ΜνΕ·ΆΤ≥ωΒΎ8Χλ Ι”Ο…®¬κ÷ßΗΕΒΡ»Υ¥ΈΈΣ331ΘΜ
Θ®2Θ©Φ«“ΜΟϊΙΥΩΆΙΚΈο÷ßΗΕΒΡΖ―”ΟΈΣ![]() Θ§
Θ§
‘ρ![]() ΒΡ»Γ÷ΒΩ…ΡήΈΣΘΚ
ΒΡ»Γ÷ΒΩ…ΡήΈΣΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΘΜ
ΘΜ
![]() ΘΜ
ΘΜ![]() ΘΜ
ΘΜ
![]() ΘΜ
ΘΜ![]()
Ζ÷≤ΦΝ–ΈΣΘΚ
|
|
|
|
|
|
|
|
|
|
Υυ“‘Θ§“ΜΟϊΙΥΩΆΙΚΈοΒΡΤΫΨυΖ―”ΟΈΣΘΚ
![]() Θ®‘ΣΘ©
Θ®‘ΣΘ©