题目内容
一个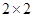 的矩阵
的矩阵 有两个特征值:
有两个特征值: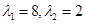 ,它们对应的一个特征向量分别为:
,它们对应的一个特征向量分别为:
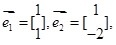 求矩阵M.
求矩阵M.
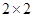 的矩阵
的矩阵 有两个特征值:
有两个特征值: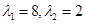 ,它们对应的一个特征向量分别为:
,它们对应的一个特征向量分别为: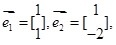 求矩阵M.
求矩阵M.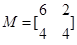
试题分析:解:设
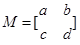 ,则
,则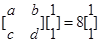 ,
,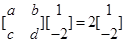 3分
3分得:
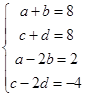 7分
7分解得:
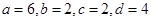 ,所以
,所以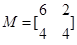 10分
10分点评:主要是考察了矩阵的求解和简单的运用,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
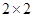 的矩阵
的矩阵 有两个特征值:
有两个特征值: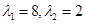 ,它们对应的一个特征向量分别为:
,它们对应的一个特征向量分别为: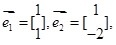 求矩阵M.
求矩阵M.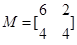
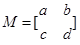 ,则
,则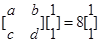 ,
,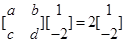 3分
3分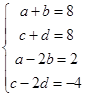 7分
7分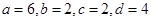 ,所以
,所以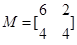 10分
10分
 名校课堂系列答案
名校课堂系列答案