Question

18．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F₁、F₂，焦距为2，过F₁作直线与椭圆交于B，D两点，且△F₂BD的周长为4$\sqrt{3}$．
（1）求椭圆方程；
（2）过F₂作垂直于BD的直线交椭圆于A，C，设逆时针连接四个交点所得四边形的面积为S，求S的取值范围．

Answer 1

分析 （1）由题意可得：$\left\{\begin{array}{l}{2c=2}\\{2a=4\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$，解出即可得出．
（2）①当BD⊥x轴时，把x=-1代入椭圆方程可得：$\frac{1}{3}+\frac{{y}^{2}}{2}$=1，解得y，可得|BD|．|AC|=2a．利用S=$\frac{1}{2}$|BD||AC|可得．
②当直线BD的斜率存在且不为0时，设直线BD的方程为：y=k（x+1），直线AC的方程为：y=-$\frac{1}{k}$（x-1）．设（x_i，y_i）（i=1，2，3，4）分别为B，D，A，C的坐标．
分别与椭圆方程联立化为（2+3k²）x²+6k²x+3k²-6=0，利用根与系数的关系可得：|BD|=$\sqrt{（1+{k}^{2}）[（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}]}$．|AC|．利用S=$\frac{1}{2}$|BD||AC|及其基本不等式的性质即可得出．

解答 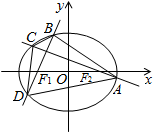解：（1）由题意可得：$\left\{\begin{array}{l}{2c=2}\\{2a=4\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$，解得c=1，a=$\sqrt{3}$，b=$\sqrt{2}$．
∴椭圆的方程为：$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$．
（2）①当BD⊥x轴时，把x=-1代入椭圆方程可得：$\frac{1}{3}+\frac{{y}^{2}}{2}$=1，解得y=$±\frac{2\sqrt{3}}{3}$，∴|BD|=$\frac{4\sqrt{3}}{3}$．
|AC|=2a=2$\sqrt{3}$．
∴S=$\frac{1}{2}$|BD||AC|=$\frac{1}{2}×\frac{4\sqrt{3}}{3}×2\sqrt{3}$=4．
②当直线BD的斜率存在且不为0时，设直线BD的方程为：y=k（x+1），直线AC的方程为：y=-$\frac{1}{k}$（x-1）．
设（x_i，y_i）（i=1，2，3，4）分别为B，D，A，C的坐标．
联立$\left\{\begin{array}{l}{y=k（x+1）}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$，化为（2+3k²）x²+6k²x+3k²-6=0，
△＞0，
∴x₁+x₂=$\frac{-6{k}^{2}}{2+3{k}^{2}}$，x₁x₂=$\frac{3{k}^{2}-6}{2+3{k}^{2}}$，
∴|BD|=$\sqrt{（1+{k}^{2}）[（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}]}$=$\frac{4\sqrt{3}（1+{k}^{2}）}{2+3{k}^{2}}$．
同理可得：|AC|=$\frac{4\sqrt{3}（1+{k}^{2}）}{3+2{k}^{2}}$．
∴S=$\frac{1}{2}$|BD||AC|=$\frac{1}{2}$$\frac{4\sqrt{3}（1+{k}^{2}）}{2+3{k}^{2}}$×$\frac{4\sqrt{3}（1+{k}^{2}）}{3+2{k}^{2}}$=$\frac{24（1+{k}^{2}）^{2}}{（2+3{k}^{2}）（3+2{k}^{2}）}$=$\frac{24}{6+\frac{1}{{k}^{2}+\frac{1}{{k}^{2}}+2}}$≥$\frac{96}{25}$，且S＜4．
综上可得：S的取值范围是$[\frac{96}{25}，4]$．

点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、弦长公式、四边形的面积、基本不等式的性质，考查了分类讨论方法、推理能力与计算能力，属于难题．