题目内容
9. 如图,四棱锥P-ABCD,底面ABCD为正方形,平面PAD⊥平面ABCD,PA=$\sqrt{3}$,PD=1,AD=2,PH⊥AD交AD于H.
如图,四棱锥P-ABCD,底面ABCD为正方形,平面PAD⊥平面ABCD,PA=$\sqrt{3}$,PD=1,AD=2,PH⊥AD交AD于H.(1)若PA,PC的中点分别为M,N,求证:MN⊥PH.
(2)求二面角A-PB-C的余弦值.
分析 (1)由已知得PH⊥平面ABCD,由此能证明MN⊥PH.
(2)以H为原点,HA为x轴,在平面ABCD内过H作AD的垂线为y轴,HP为z轴,建立空间直角坐标系,利用向量法能求出二面角A-PB-C的余弦值.
解答 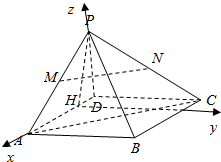 (1)证明:∵底面ABCD为正方形,平面PAD⊥平面ABCD,
(1)证明:∵底面ABCD为正方形,平面PAD⊥平面ABCD,
PA=$\sqrt{3}$,PD=1,AD=2,PH⊥AD交AD于H,
∴PH⊥平面ABCD,∵AC?平面ABCD,∴PH⊥AC,
∵PA,PC的中点分别为M,N,∴MN∥AC,
∴MN⊥PH.
(2)∵底面ABCD为正方形,平面PAD⊥平面ABCD,
PA=$\sqrt{3}$,PD=1,AD=2,PH⊥AD交AD于H,
∴AD2=PA2+PD2,
∴PH=$\frac{PA×PD}{AD}$=$\frac{\sqrt{3}×1}{2}$=$\frac{\sqrt{3}}{2}$,AH=$\sqrt{3-\frac{3}{4}}$=$\frac{3}{2}$,DH=2-$\frac{3}{2}=\frac{1}{2}$,
以H为原点,HA为x轴,在平面ABCD内过H作AD的垂线为y轴,HP为z轴,建立空间直角坐标系,
则A($\frac{3}{2}$,0,0),P(0,0,$\frac{\sqrt{3}}{2}$),B($\frac{3}{2}$,2,0),C(-$\frac{1}{2}$,2,0),
$\overrightarrow{PA}$=($\frac{3}{2},0,-\frac{\sqrt{3}}{2}$),$\overrightarrow{PB}$=($\frac{3}{2},2,-\frac{\sqrt{3}}{2}$),$\overrightarrow{PC}$=(-$\frac{1}{2}$,2,-$\frac{\sqrt{3}}{2}$),
设平面PAB的法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PA}=\frac{3}{2}x-\frac{\sqrt{3}}{2}z=0}\\{\overrightarrow{m}•\overrightarrow{PB}=\frac{3}{2}x+2y-\frac{\sqrt{3}}{2}z=0}\end{array}\right.$,取x=1,得$\overrightarrow{m}$=(1,0,$\sqrt{3}$),
设平面PBC的法向量$\overrightarrow{n}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=\frac{3}{2}a+2b-\frac{\sqrt{3}}{2}c=0}\\{\overrightarrow{n}•\overrightarrow{PC}=-\frac{1}{2}a+2b-\frac{\sqrt{3}}{2}c=0}\end{array}\right.$,取b=$\sqrt{3}$,得$\overrightarrow{n}$=(0,$\sqrt{3}$,4),
设二面角A-PB-C的平面角为θ,
cosθ=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$|=|$\frac{4\sqrt{3}}{2\sqrt{19}}$|=$\frac{2\sqrt{57}}{19}$,
∴二面角A-PB-C的余弦值为$\frac{2\sqrt{57}}{19}$.
点评 本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 名校课堂系列答案
名校课堂系列答案| A. | A⊆B | B. | B⊆A | ||
| C. | A∩B=∅ | D. | 集合A、B间没有包含关系 |
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 相交但不垂直 |

 如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$.CF与平面 ABCD垂直,CF=2.求二面角B-AF-D的大小.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$.CF与平面 ABCD垂直,CF=2.求二面角B-AF-D的大小. 三棱锥P-ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证:
三棱锥P-ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证: