题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,连接椭圆的四个顶点得到的四边形的面积为
,连接椭圆的四个顶点得到的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 为坐标原点,取
为坐标原点,取![]() 上不同于
上不同于![]() 的点
的点![]() ,以
,以![]() 为直径作圆与
为直径作圆与![]() 相交另外一点
相交另外一点![]() ,求该圆面积的最小值时点
,求该圆面积的最小值时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)借助题设条件建立方程组求解;(2)运用抛物线的定义求解;(3)借助题设运用圆与抛物线的位置关系探求.
试题解析:
(1)由![]() ,得
,得![]() ,再由
,再由![]() ,解得
,解得![]() ……………………1分
……………………1分
由题意可知![]() ,即
,即![]() …………………………………………………2分
…………………………………………………2分
解方程组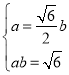 得
得![]() ,
,![]() ……………………………………………………3分
……………………………………………………3分
所以椭圆![]() 的方程是
的方程是![]() ……………………………………………………………4分
……………………………………………………………4分
(2)因为![]() ,所以动点
,所以动点![]() 到定直线
到定直线![]() :
:![]() 的距离等于它到定点
的距离等于它到定点![]() 的距离,所以动点
的距离,所以动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为准线,
为准线,![]() 为焦点的抛物线,…………………………………………6分
为焦点的抛物线,…………………………………………6分
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ………………………………………………………7分
………………………………………………………7分
(3)因为以![]() 为直径的圆与
为直径的圆与![]() 相交于点
相交于点![]() ,所以
,所以![]() ,即
,即![]() …8分
…8分
设![]() ,
,![]() ,
,![]() ,
,![]()
所以![]()
因为![]() ,
,![]() ,化简得
,化简得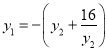 ……………………………………9分
……………………………………9分
所以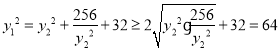 ,
,
当且仅当![]() 即
即![]() ,
,![]() 时等号成立.…………………………10分
时等号成立.…………………………10分
圆的直径![]()
因为![]() ,所以当
,所以当![]() 即
即![]() 时,
时,![]() ,…………………11分
,…………………11分
所以所求圆的面积的最小时,点![]() 的坐标为
的坐标为![]() ………………………………12分
………………………………12分

练习册系列答案
相关题目