题目内容
(本题满分10分)
已知函数f (x)=| x-a | + | x + 2 |(a为常数,且a∈R).
(Ⅰ)若函数f (x)的最小值为2,求a的值;
(Ⅱ)当a=2时,解不等式f (x)≤6.
已知函数f (x)=| x-a | + | x + 2 |(a为常数,且a∈R).
(Ⅰ)若函数f (x)的最小值为2,求a的值;
(Ⅱ)当a=2时,解不等式f (x)≤6.
(1) a=0或a=-4(2) [-3,3]
试题分析:解:(Ⅰ)f (x)=|x-a|+|x+2|=| a-x |+|x+2|
≥|a-x+x+2|=|a+2|,
由|a+2|=2,解得a=0或a=-4. ……5分
(Ⅱ)f (x)= |x-2|+|x+2|.
当x<-2时,不等式为2-x-x-2≤6,其解为-3≤x<-2;
当-2≤x<2时,不等式为2-x+x+2≤6恒成立,其解为-2≤x<2;
当x≥2时,不等式为x-2+x+2≤6,其解为2≤x≤3;
所以不等式f (x)≤6的解集为[-3,3]. ……10分
如有其它解法,相应给分.
点评:零点分段论是解决多个绝对值的函数的一般方法,同时能利用分段函数的性质,求解最值,属于基础题。

练习册系列答案
相关题目
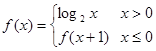 ,则
,则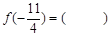
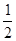
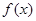 为定义在
为定义在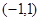 上的奇函数,当
上的奇函数,当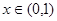 时,
时,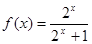
 是增函数(2)求
是增函数(2)求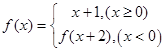 ,则
,则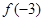 ________._
________._ 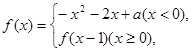
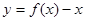 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数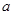 的取值范围是( )
的取值范围是( )
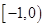
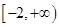
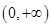
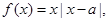 若对任意的
若对任意的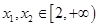 ,且
,且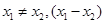
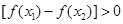 恒成立,则实数a的取值范围为 。
恒成立,则实数a的取值范围为 。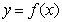 是定义在
是定义在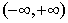 上的偶函数,当
上的偶函数,当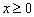 时,
时, 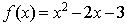 。
。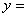
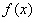 在
在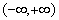 上的解析式;
上的解析式; 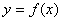 的大致图象;并根据图像写出
的大致图象;并根据图像写出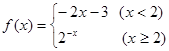 ,则
,则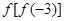 的值为 .
的值为 .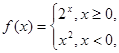 则
则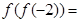 ( )
( )