题目内容
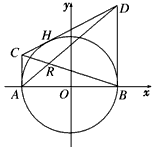
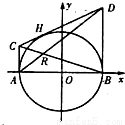
如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.(I)求动点R的轨迹E的方程;
(II)设E的上顶点为M,直线l交曲线E于P、Q两点,问:是否存在这样的直线l,使点G(1,0)恰为△PQM的垂心?若存在,求出直线l的方程,若不存在,说明理由.
【答案】分析:(I)因为动点R为动直线直线AD、BC的交点,所以可用消参法求R的轨迹方程.先设点H(x,y),求出A,B,C,D四点坐标,则可得到含参数x,y的直线AD,BC方程,再消去参数,即可得到求动点R的轨迹E的方程.
(II)假设存在直线l交曲线E于P、Q两点,使点G(1,0)恰为△PQM的垂心.则MG为△PQM在边PQ上的高线所在直线,MG⊥PQ,又因为kMG=-1,所以kPQ=1,这样,就可设出直线MQ的方程为y=x+m,与曲线E的方程联立,消y,得到关于x的一元二次方程,求两根之和,两根之积.又因为点G(1,0)恰为△PQM的垂心,所以MP⊥GQ,∴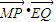 =0,得到含x1,x2的方程,根据前面所求的x1+x2,x1x2,就可求m的值,如能求出,则m存在,否则,m不存在
=0,得到含x1,x2的方程,根据前面所求的x1+x2,x1x2,就可求m的值,如能求出,则m存在,否则,m不存在
解答:解:(I)则x2+y2=4,
由题意可知,y≠0,且以H为切点的圆的切线斜率为:-
故切线方程为:y-y=- (x-x),
(x-x),
展开得,xx+yy=x2+y2即以H为切点的圆的方程为xx+yy=4
∵A(-2,0),B(2,0)将x=±2代入上述方程可得点C,D坐标分别为C(-2,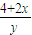 )D(2,
)D(2,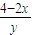 )
)
则lAD: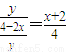 ,lBC:
,lBC: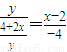 两式相乘,可消x,y,
两式相乘,可消x,y,
化简得动点R的轨迹E的方程为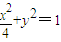
(II)假设存在直线l交曲线E于P、Q两点,使点G(1,0)恰为△PQM的垂心.
设P(x1,y1),Q(x1,y2)∵M(0,1),G(1,0),MG⊥PQ,∴kPQ=1
设直线l为y=x+m,与曲线E的方程联立,消y,得5x2+8mx+4m2-4=0
由△=(8m)2-4×5(4m2-4)>0得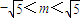
x1+x2=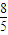 m,x1x2=
m,x1x2=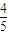 (m2-1)
(m2-1)
又∵MP⊥GQ,∴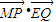 =0
=0
∴x1(x2-1)+y1(y2-1)=0
又y1=x1+m,y2=x2+m
∴x1(x2-1)+(x2+m)(x1+m-1)=,0即2x1x2+(x1+x2)(m-1)+m2-m=0
∴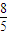 (m2-1)-
(m2-1)- m(m-1)+m2-m=0即5m2-3m-8=0
m(m-1)+m2-m=0即5m2-3m-8=0
解得m=1或m=-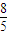
检验:当m=1时,l过M点,构不成三角形,舍去.当m=-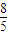 时,符合条件
时,符合条件
故直线l的方程为y=x-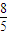
点评:本题考查了消参法求动点轨迹方程,以及直线与椭圆位置关系的判断,计算量较大,应认真计算.
(II)假设存在直线l交曲线E于P、Q两点,使点G(1,0)恰为△PQM的垂心.则MG为△PQM在边PQ上的高线所在直线,MG⊥PQ,又因为kMG=-1,所以kPQ=1,这样,就可设出直线MQ的方程为y=x+m,与曲线E的方程联立,消y,得到关于x的一元二次方程,求两根之和,两根之积.又因为点G(1,0)恰为△PQM的垂心,所以MP⊥GQ,∴
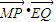 =0,得到含x1,x2的方程,根据前面所求的x1+x2,x1x2,就可求m的值,如能求出,则m存在,否则,m不存在
=0,得到含x1,x2的方程,根据前面所求的x1+x2,x1x2,就可求m的值,如能求出,则m存在,否则,m不存在解答:解:(I)则x2+y2=4,
由题意可知,y≠0,且以H为切点的圆的切线斜率为:-

故切线方程为:y-y=-
 (x-x),
(x-x),展开得,xx+yy=x2+y2即以H为切点的圆的方程为xx+yy=4
∵A(-2,0),B(2,0)将x=±2代入上述方程可得点C,D坐标分别为C(-2,
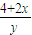 )D(2,
)D(2,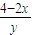 )
)则lAD:
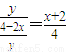 ,lBC:
,lBC: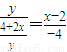 两式相乘,可消x,y,
两式相乘,可消x,y,化简得动点R的轨迹E的方程为
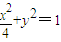
(II)假设存在直线l交曲线E于P、Q两点,使点G(1,0)恰为△PQM的垂心.
设P(x1,y1),Q(x1,y2)∵M(0,1),G(1,0),MG⊥PQ,∴kPQ=1
设直线l为y=x+m,与曲线E的方程联立,消y,得5x2+8mx+4m2-4=0
由△=(8m)2-4×5(4m2-4)>0得
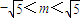
x1+x2=
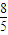 m,x1x2=
m,x1x2=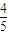 (m2-1)
(m2-1)又∵MP⊥GQ,∴
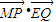 =0
=0∴x1(x2-1)+y1(y2-1)=0
又y1=x1+m,y2=x2+m
∴x1(x2-1)+(x2+m)(x1+m-1)=,0即2x1x2+(x1+x2)(m-1)+m2-m=0
∴
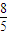 (m2-1)-
(m2-1)- m(m-1)+m2-m=0即5m2-3m-8=0
m(m-1)+m2-m=0即5m2-3m-8=0解得m=1或m=-
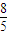
检验:当m=1时,l过M点,构不成三角形,舍去.当m=-
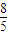 时,符合条件
时,符合条件故直线l的方程为y=x-
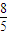
点评:本题考查了消参法求动点轨迹方程,以及直线与椭圆位置关系的判断,计算量较大,应认真计算.

练习册系列答案
相关题目
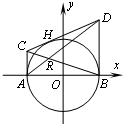 如图,过圆x2+y2=4与x的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R.
如图,过圆x2+y2=4与x的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R. (2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.
(2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.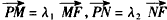 ,求证:λ1+λ2为定值。
,求证:λ1+λ2为定值。 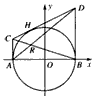
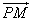 =λ1
=λ1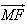 ,
, =λ2
=λ2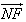 ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.