题目内容
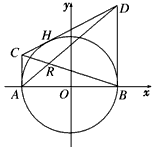
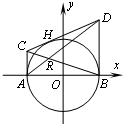 如图,过圆x2+y2=4与x的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R.
如图,过圆x2+y2=4与x的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R.(1)求动点R的轨迹E方程;
(2)过曲线E的右焦点作直线l交曲线E于M、N两点,交y轴于P点,记
| PM |
| MF |
| PN |
| NF |
分析:(1)设H点的坐标为(x0,y0),则x02+y02=4.由题意得以H为切点的圆的切线的方程为x0x+y0y=4.进而求出点C,D的坐标,可求出直线AD与BC的方程,联立两条直线的方程可得动点R的轨迹方程.
(2)由(1)得曲线E是焦点在x轴上的椭圆且其右焦点为F(
,0),分情况讨论①当直线l的斜率为0时,M,N,P三点在x轴上,得M,N,P的坐标进而表示出λ1+λ2的数值.②当直线l的斜率不为0时,设直线MN的方程为:x=my+
,则点P的坐标为(0,-
),且设点M(x1,y1),N(x2,y2).再表达出λ1+λ2的表达式结合着根与系数的关系得到其为定值-8.
(2)由(1)得曲线E是焦点在x轴上的椭圆且其右焦点为F(
| 3 |
| 3 |
| ||
| m |
解答:解:(1)设H点的坐标为(x0,y0),则x02+y02=4
由题意得y0≠0,且以H为切点的圆的切线的斜率为:-
,
故切线的方程为:y-y0=-
(x-x0)
即以H为切点的圆的切线方程为:x0x+y0y=4.
∵A(-2,0),B(2,0)将x=±2代入上述方程得C(-2,
),D(2,
)
则直线AD的方程为:
=
,直线BC的方程为:
=
,
将两式相乘并化简得动点R的轨迹方程为:
+y2=1.
(2)由(1)得曲线E是焦点在x轴上的椭圆且其右焦点为F(
,0),
①当直线l的斜率为0时,M,N,P三点在x轴上,
不妨设M(2,0),N(-2,0)且P(0,0),此时有|PM|=2,|MF|=2-
,|PN|=2,|NF|=2+
所以λ1+λ2=
+
=
-
=-
-
=-8.
②当直线l的斜率不为0时,设直线MN的方程为:x=my+
则点P的坐标为(0,-
),且设点M(x1,y1),N(x2,y2)
联立
消去x可得:(m2+4)y2+2
my-1=0
则y1+ y2=
,y1y2=
所以λ1+λ2=
+
=-2-
•
=-8.
所以λ1+λ2为定值为-8.
由题意得y0≠0,且以H为切点的圆的切线的斜率为:-
| x0 |
| y0 |
故切线的方程为:y-y0=-
| x0 |
| y0 |
即以H为切点的圆的切线方程为:x0x+y0y=4.
∵A(-2,0),B(2,0)将x=±2代入上述方程得C(-2,
| 4+2x0 |
| y0 |
| 4-2x0 |
| y0 |
则直线AD的方程为:
| y | ||
|
| x+2 |
| 4 |
| y | ||
|
| x+2 |
| -4 |
将两式相乘并化简得动点R的轨迹方程为:
| x2 |
| 4 |
(2)由(1)得曲线E是焦点在x轴上的椭圆且其右焦点为F(
| 3 |
①当直线l的斜率为0时,M,N,P三点在x轴上,
不妨设M(2,0),N(-2,0)且P(0,0),此时有|PM|=2,|MF|=2-
| 3 |
| 3 |
所以λ1+λ2=
| ||
|
| ||
|
| |PM| |
| |MF| |
| |PN| |
| |NF| |
| 2 | ||
2-
|
| 2 | ||
2+
|
②当直线l的斜率不为0时,设直线MN的方程为:x=my+
| 3 |
则点P的坐标为(0,-
| ||
| m |
联立
|
| 3 |
则y1+ y2=
-2
| ||
| m2+4 |
| -1 |
| m2+4 |
所以λ1+λ2=
y1+
| ||||
| - y1 |
y2+
| ||||
| -y2 |
| ||
| m |
| y1+y2 |
| y1y2 |
所以λ1+λ2为定值为-8.
点评:定值、定点问题是高考考查的重点,此类问题多与直线方程、圆锥曲线方程有关,解决此类问题得到关键是根据题意结合根与系数的关系正确的表达出λ1+λ2的表达式,进行化简可得定值.

练习册系列答案
相关题目
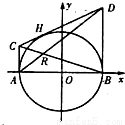
 (2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.
(2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.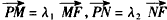 ,求证:λ1+λ2为定值。
,求证:λ1+λ2为定值。 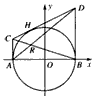
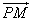 =λ1
=λ1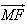 ,
, =λ2
=λ2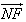 ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.