题目内容

1．若${2^{{{log}_3}x}}$=$\frac{1}{8}$，则x=$\frac{1}{27}$．

分析 利用指数与对数的运算性质即可得出．

解答 解：∵${2^{{{log}_3}x}}$=$\frac{1}{8}$，∴${2^{{{log}_3}x}}$=2-3，∴log3x=-3，∴x=3-3=$\frac{1}{27}$，
故答案为：$\frac{1}{27}$．

点评 本题考查了指数与对数的运算性质，属于基础题．

练习册系列答案
相关题目
10．已知a＞0，函数f（x）=$\frac{|x-2a|}{x+2a}$在区间[1，4]上的最大值等于$\frac{1}{3}$，则a的值为（　　）
A．$\frac{1}{4}$B．1C．2D．4
12．已知椭圆C的方程为：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），椭圆的左右焦点F1，F2与其短轴的端点构成等边三角形，且满足a2=4c（c是椭圆C的半焦距）．
（1）求椭圆C的方程；
（2）设直线l：3x-2y=0与椭圆C在x轴上方的一个交点为P，F是椭圆的右焦点，试探究以PF为直径的圆与以椭圆长轴为直径的圆的位置关系．
9．对于n∈N+，将n表示为n=a${\;}_{0}×{2}^{k}$+a1×2k-1+a2×2k-2+…+ak-1×21+ak×20，当i=0时，a1=1，当1≤i≤k时，a1为0或1，记I（n）为上诉表示中ai为0个数（例如：1-1×20，4=1×22+0×21+0×00，故I（1）=0，I（4）=2），则
（1）I（15）=0
（2）$\underset{\stackrel{126}{∑}}{n=1}$2I（n）=1092．
16．函数f（x）=3x+x-3的零点所在的区间是（　　）
A．（-2，-1）B．（-1，0）C．（0，1）D．（1，2）
6．设a，b∈R，则“a＜b”是“（a-b）a2＜0”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件
13．某地近几年粮食需求量逐年上升，下表是部分统计数据：
年份20062008201020122014
年需求量（万吨）257276298298318
（1）利用所给数据求年需求量与年份之间的回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（2）利用（1）中所求出的直线方程预测该地2015年的粮食需求量．
10．以下个数有可能是五进制数的是（　　）
A．15B．106C．731D．21340
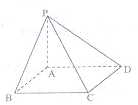11．如图，正方形ABCD所在平面外有一点P，PA⊥平面ABCD，若PA=AB，则平面PAB与平面PCD所成的角为45°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网