题目内容
11.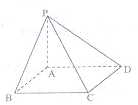 如图,正方形ABCD所在平面外有一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD所成的角为45°.
如图,正方形ABCD所在平面外有一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD所成的角为45°.
分析 建立以A为原点的空间坐标系,利用向量法求出平面的法向量,即可得到结论.
解答 解: ∵正方形ABCD所在平面外有一点P,PA⊥平面ABCD,若PA=AB,
∵正方形ABCD所在平面外有一点P,PA⊥平面ABCD,若PA=AB,
∴建立以A为坐标原点,AB,AD,AP分别为x,y,z轴的空间坐标系如图:
设AB=PA=1,
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,1),
则$\overrightarrow{PC}$=(1,1,-1),$\overrightarrow{DC}$=(1,0,0),
则$\overrightarrow{AD}$=(0,1,0)是平面PAB的法向量,
平面PCD的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{PC}•\overrightarrow{n}=x+y-z=0}\\{\overrightarrow{DC}•\overrightarrow{n}=x=0}\end{array}\right.$,
令y=1,则z=1,x=0,即$\overrightarrow{n}$=(0,1,1),
则$\overrightarrow{AD}$•$\overrightarrow{n}$=1,
则cos<$\overrightarrow{AD}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{AD}•\overrightarrow{n}}{|\overrightarrow{AD}||\overrightarrow{n}|}$=$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,
则<$\overrightarrow{AD}$,$\overrightarrow{n}$>=45°,
故平面PAB与平面PCD所成的角为45°,
故答案为:45°
点评 本题主要考查二面角的求解,建立坐标系,利用向量法是解决二面角的基本方法.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{6}{5}$ | D. | $\frac{2}{3}$ |
| A. | 若¬p,则q | B. | 若p,则¬q | C. | 若¬p,则¬q | D. | 若q,则p |
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |