题目内容
抛物线y2=2px(p>0)上有一点M，它的横坐标是3,它到焦点的距离是5,则抛物线方程为( A )
| A．y2=8x | B．y2=4x | C．y2=3x | D．y2=2x |
A
解析试题分析：
,
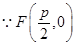
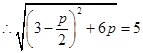
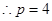
考点：抛物线定义
点评：本题还可以用抛物线定义直接求出准线，进一步求方程
练习册系列答案
相关题目
一动圆圆心在抛物线
上,且动圆恒与直线
相切,则动圆必过定点
A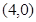． | B． | C． | D． |
，
)，P2的柱坐标是P2(2，
，1)，则|P1P2|=( )
过点(0，1)作直线，使它与抛物线y2=4x仅有一个公共点，这样的直线有( )
| A．1条 | B．2条 | C．3条 | D．4条 |
直线
与曲线
相切于点
，则
的值为 ( )
| A．－3 | B．9 |
| C．－15 | D．－7 |
等轴双曲线x2-y2=a2与直线y=ax(a>0)没有公共点，则a的取值范围( )
| A．a=1 | B．0<a<1 | C．a>1 | D．a≥1 |
若点P是曲线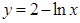
上任意一点，则点P到直线
的最小距离是（ ）
A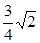． | B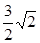． | C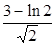． | D． |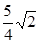
焦点坐标是
，
，且虚轴长为
的双曲线的方程是( )
A． | B． |
C． | D． |
已知曲线C: 
与抛物线
的一个交点为M，
为抛物线的焦点，若
，则b的值为
A． | B．－ | C． | D．－ |