题目内容
【题目】已知数列{an}的首项为1,若对任意的n∈N*,数列{an}满足an+1﹣3an<2,则称数列{an}具有性质L.
(Ⅰ)判断下面两个数列是否具有性质L:
①1,3,5,7,9,…;
②1,4,16,64,256,…;
(Ⅱ)若{an}是等差数列且具有性质L,其前n项和Sn满足Sn<2n2+2n(n∈N*),求数列{an}的公差d的取值范围;
(Ⅲ)若{an}是公比为正整数的等比数列且具有性质L,设bn=an![]() (n∈N*),且数列{bn}不具有性质L,求数列{an}的通项公式.
(n∈N*),且数列{bn}不具有性质L,求数列{an}的通项公式.
【答案】(Ⅰ)1,3,5,7,9,…具有性质L,理由见解析;(Ⅱ)[0,4);(Ⅲ)![]() .
.
【解析】
(Ⅰ)根据题意利用an+1﹣3an<2,验证即可
(Ⅱ)利用等差数列的通项公式以及前![]() 项和公式,代入不等式即可求解.
项和公式,代入不等式即可求解.
(Ⅲ)利用等比数列的通项公式求出数列{an}的公比![]() ,{bn}不具有性质L,只需存在正整数m,使得bm+1﹣3bm≥2,
,{bn}不具有性质L,只需存在正整数m,使得bm+1﹣3bm≥2,![]() ,,进而可确定
,,进而可确定![]() ,利用等比数列的通项公式即可求解.
,利用等比数列的通项公式即可求解.
(Ⅰ)①1,3,5,7,9,…具有性质L.
理由如下:
对于数列1,3,5,7,9,…,其通项公式为an=2n﹣1,n∈N*,
an+1﹣3an=2n+1﹣3(2n﹣1)=4﹣4n<2,
∴1,3,5,7,9,…具有性质L.
②1,4,16,64,256,…不具有性质L.
理由如下:
对于数列1,4,16,64,256,…,
∵a3﹣3a2=16﹣3×4=4>2,
∴1,4,16,64,256,…不具有性质L.
(Ⅱ)∵等差数列{an}具有性质L,∴an+1﹣3an<2,
即1+nd﹣3[1+(n﹣1)d]<2对n∈N*均成立,
∴(3﹣2n)d<4对n∈N*均成立,当n=1时,d<4,
当n≥2时,d![]() 恒成立,
恒成立,
而![]() 0,(n≥2,n∈N*),∴d≥0,∴0≤d<4,
0,(n≥2,n∈N*),∴d≥0,∴0≤d<4,
∵a1=1,得![]() ,
,
∴由题意n![]() 2n2+2n对n∈N*均成立,
2n2+2n对n∈N*均成立,
∴当n=1时,d∈R,当n≥2时,d![]() 恒成立,
恒成立,
∵![]() 4,∴d≤4.
4,∴d≤4.
∵![]() ,(n≥2,n∈N*),∴d≥0.∴0≤d<4,
,(n≥2,n∈N*),∴d≥0.∴0≤d<4,
综上,0≤d<4.
∴数列{an}的公差d的取值范围是[0,4).
(Ⅲ)设数列{an}的公比为q,则![]() qn﹣1,
qn﹣1,
∵公比为正整数的等比数列{an}具有性质L,
∴qn﹣3qn﹣1<2,∴(q﹣3)qn﹣1<2,∴q﹣3≤0,
若不然,q≥4,此时,(q﹣3)qn﹣1≥4n﹣1,不满足条件,
∵q是正整数,∴q=1,2,3,
∵{bn}不具有性质L,∴存在正整数m,使得bm+1﹣3bm≥2,
∴![]() 2,(
2,(![]() )
)![]() 2,
2,
∴![]() ,∴
,∴![]() ,
,
∵q∈{1,2,3}.∴q=3,
当q=3时,![]() ,满足an+1﹣3an<2.
,满足an+1﹣3an<2.
∴数列{an}的通项公式为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
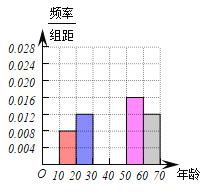
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.