题目内容
已知三角形的三个顶点是A(4,0),B(6,6),C(0,2).
(1)求AB边上的高所在直线的方程;
(2)求AC边上的中线所在直线的方程.
(1)x+3y﹣6=0;(2)5x﹣4y﹣5=0.
解析试题分析:
解题思路:(1)因为AB边上的高所在直线经过点C(0,2),且与AB垂直,所以先求出AB的斜率,再根据垂直求出CD的斜率,然后写出直线的点斜式方程,化成一般式即可;(2)因为AC边上的中线所在直线经过点B与CD 的中点,所以先求出CD的中点坐标,写出直线的两点式方程,化成一般式即可.
规律总结:求直线方程,要根据题意恰当地设出直线方程的形式(点斜式、斜截式、两点式、截距式、一般式),再利用直线间的位置关系(平行、垂直、相交)进行求解.
试题解析:(1)∵A(4,0),B(6,6),C(0,2),∴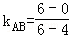 =3,
=3,
∴AB边上的高所在直线的斜率k=﹣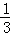 ,
,
∴AB边上的高所在直线的方程为y﹣2=﹣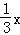 ,整理,得x+3y﹣6=0.
,整理,得x+3y﹣6=0.
(2)∵AC边的中点为(2,1),
∴AC边上的中线所在的直线方程为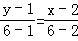 ,
,
整理,得5x﹣4y﹣5=0.
考点:1.直线方程;2.中点坐标公式;3.两直线间的位置关系.

练习册系列答案
相关题目
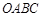 的顶点
的顶点 为原点,
为原点,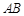 边所在直线的方程为
边所在直线的方程为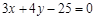 ,顶点
,顶点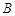 的纵坐标为
的纵坐标为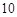 .
.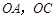 边所在直线的方程;
边所在直线的方程;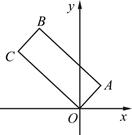
 中,原点为
中,原点为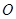 ,抛物线
,抛物线 的方程为
的方程为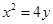 ,线段
,线段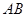 是抛物线
是抛物线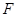 ;
;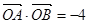 ,求证:直线
,求证:直线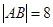 时,设圆
时,设圆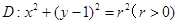 ,若存在且仅存在两条动弦
,若存在且仅存在两条动弦 相切,求半径
相切,求半径 的取值范围?
的取值范围?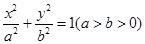 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率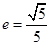 , 直线
, 直线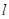 交椭圆于M,N两点.
交椭圆于M,N两点.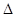 BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线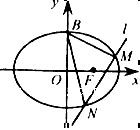
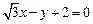 的倾斜角为 ▲
的倾斜角为 ▲ 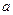 = 时,直线
= 时,直线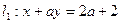 ,直线
,直线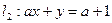 平行.
平行.