题目内容
在平面直角坐标系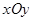 中,原点为
中,原点为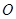 ,抛物线
,抛物线 的方程为
的方程为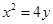 ,线段
,线段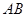 是抛物线
是抛物线 的一条动弦.
的一条动弦.
(1)求抛物线 的准线方程和焦点坐标
的准线方程和焦点坐标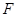 ;
;
(2)若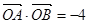 ,求证:直线
,求证:直线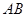 恒过定点;
恒过定点;
(3)当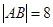 时,设圆
时,设圆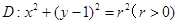 ,若存在且仅存在两条动弦
,若存在且仅存在两条动弦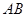 ,满足直线
,满足直线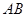 与圆
与圆 相切,求半径
相切,求半径 的取值范围?
的取值范围?
(1)准线方程: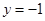 ,焦点坐标
,焦点坐标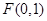 ;(2)证明见解析;(3)
;(2)证明见解析;(3)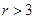 .
.
解析试题分析:(1)根据抛物线标准方程确定焦点在哪个轴上及开口方向,焦点为 ,准线方程为
,准线方程为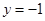 ;(2)本题实质是直线与抛物线相交问题,一般是设直线
;(2)本题实质是直线与抛物线相交问题,一般是设直线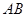 方程为
方程为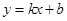 ,与抛物线方程联立方程组,消去
,与抛物线方程联立方程组,消去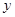 可得
可得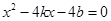 ,再设
,再设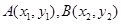 ,则有
,则有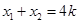 ,
,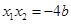 ,而
,而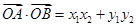 ,把刚才求出的
,把刚才求出的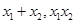 代入可得
代入可得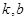 的关系,本题中求得
的关系,本题中求得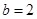 为常数,因此直线
为常数,因此直线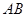 A一定过定点
A一定过定点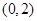 ;(3)由(2)利用
;(3)由(2)利用 可求出
可求出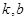 的关系式,
的关系式,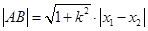
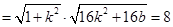 ,则
,则 ,而直线
,而直线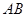 与圆相切,则圆心到直线的距离
与圆相切,则圆心到直线的距离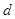 等于圆的半径
等于圆的半径 ,即
,即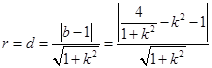 ,由题意,作为关于
,由题意,作为关于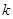 的方程,此方程只有两解,设
的方程,此方程只有两解,设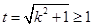 ,则有
,则有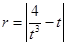 ,由于
,由于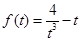 在
在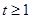 时是减函数,且
时是减函数,且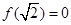 ,即函数
,即函数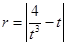 在
在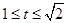 时递减
时递减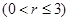 ,在
,在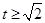 时递增
时递增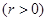 ,因此为了保证
,因此为了保证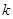 有两解,即
有两解,即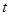 只有一解,故要求
只有一解,故要求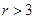 .
.
(1)准线方程: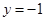 +2分 焦点坐标:
+2分 焦点坐标: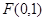 +4分
+4分
(2)设直线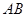 方程为
方程为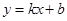 ,
,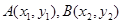
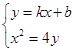 得
得 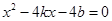
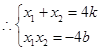 +6分
+6分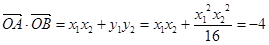
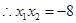
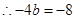 +8分
+8分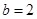 直线
直线 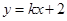 过定点(0,2) +10分
过定点(0,2) +10分
(3)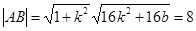
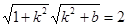 +12分
+12分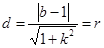 +14分
+14分 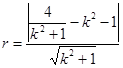 令
令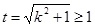
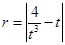 当
当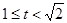 时,
时, 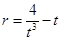 单调递减,
单调递减, +15分
+15分
当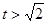 时,
时, 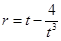 单调递增,
单调递增,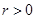 +16分
+16分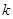 存在两解即
存在两解即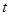 一解
一解 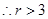 +18分
+18分
考点:(1)抛物线的性质;(2)直线与抛物线相交问题;(3)圆的切线的条数与方程的解.

练习册系列答案
相关题目
 经过点
经过点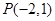 .
.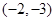 ,求直线
,求直线
 上的圆的方程.
上的圆的方程. ,且被两直线L1:
,且被两直线L1: 和 L2:
和 L2: 截得的线段AB中点恰好是点P,求直线L的方程.
截得的线段AB中点恰好是点P,求直线L的方程. ,在y轴上截得线段长为2
,在y轴上截得线段长为2 .
. ,求圆P的方程.
,求圆P的方程.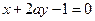 与
与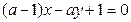 平行,则
平行,则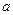 的值为 。
的值为 。