题目内容
如图,矩形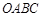 的顶点
的顶点 为原点,
为原点,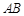 边所在直线的方程为
边所在直线的方程为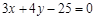 ,顶点
,顶点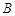 的纵坐标为
的纵坐标为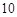 .
.
(1)求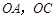 边所在直线的方程;
边所在直线的方程;
(2)求矩形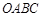 的面积.
的面积.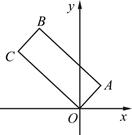
(1)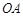 边所在直线的方程为
边所在直线的方程为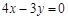 ,
, 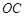 边所在直线的方程为
边所在直线的方程为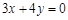 ;(2)
;(2)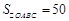 .
.
解析试题分析:(1)根据给出的条件矩形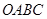 可知
可知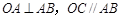 ,即有
,即有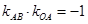 ,
,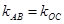 ,从而根据
,从而根据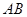 的方程为
的方程为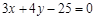 可求得
可求得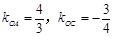 ,再由直线
,再由直线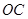 ,
,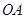 均过原点可知
均过原点可知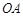 边所在直线的方程为
边所在直线的方程为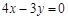 ,
, 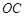 边所在直线的方程为
边所在直线的方程为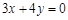 ;(2)根据条件中点
;(2)根据条件中点 的纵坐标为
的纵坐标为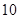 ,结合点
,结合点 在直线
在直线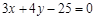 ,从而根据点到直线距离公式可求
,从而根据点到直线距离公式可求 到直线
到直线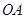 的距离即
的距离即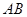 的长度,同理可求得
的长度,同理可求得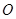 到直线
到直线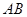 的距离即
的距离即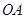 的长度,从而可求得矩形
的长度,从而可求得矩形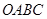 的面积.
的面积.
试题解析:(1)∵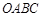 是矩形,∴
是矩形,∴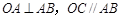 , 1分
, 1分
由直线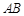 的方程
的方程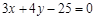 可知,
可知,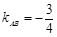 ,∴
,∴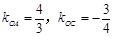 , 4分
, 4分
∴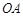 边所在直线的方程为
边所在直线的方程为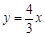 ,即
,即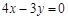 , 5分
, 5分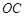 边所在直线的方程为
边所在直线的方程为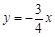 ,即
,即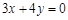 ; 6分
; 6分
(2)∵点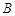 在直线
在直线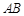 上,且纵坐标为
上,且纵坐标为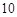 ,
,
∴点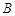 的横坐标由
的横坐标由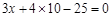 解得为
解得为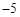 ,即
,即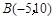 . 7分
. 7分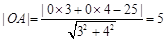 ,
,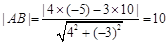 , 11分
, 11分
∴ . 12分
. 12分
考点:1.直线的方程;2.两直线的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 经过点
经过点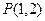 且在
且在 轴、
轴、 轴上截距互为相反数的直线方程是
轴上截距互为相反数的直线方程是 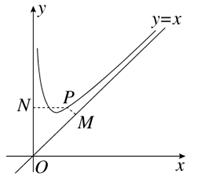

 上的圆的方程.
上的圆的方程.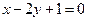 在
在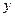 轴上的截距为 ★ .
轴上的截距为 ★ . ,直线
,直线 与
与 关于直线
关于直线 对称,则直线
对称,则直线