题目内容
【题目】已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 两点,坐标原点为
两点,坐标原点为![]() ,且
,且![]() 12.
12.
(Ⅰ)求抛物线的方程;
(Ⅱ)当以![]() 为直径的圆的面积为
为直径的圆的面积为![]() 时,求
时,求![]() 的面积
的面积![]() 的值.
的值.
【答案】(I)![]() ;(Ⅱ)
;(Ⅱ)![]() 的面积为4.
的面积为4.
【解析】试题分析:(I)将![]() 代入
代入![]() ,利用韦达定理可得,
,利用韦达定理可得,![]() ,利用
,利用![]() ,可得
,可得![]() ,代入即可得到
,代入即可得到![]() 的值;(Ⅱ)根据(I)中
的值;(Ⅱ)根据(I)中![]() 的值,将
的值,将![]() 化为
化为![]() ,可得到
,可得到![]() 的式子,由直径
的式子,由直径![]() ,解方程可求出
,解方程可求出![]() 的值,进而可求出
的值,进而可求出![]() 的面积
的面积![]() 的值.
的值.
试题解析:(I)设![]() ,代入
,代入![]() ,得
,得![]()
设点![]() ,则
,则![]() ,则
,则![]() ,
,
因为![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() .
.
所以抛物线的方程为![]() .
.
(Ⅱ)由(I)![]() 化为
化为![]() ,则
,则![]() .
.
又![]() ,
,
因为以![]() 为直径的圆的面积为
为直径的圆的面积为![]() ,
,
所以圆的半径为4,直径![]() .
.
则![]() ,得
,得![]() ,得
,得![]() ,得
,得![]() ,得
,得![]() (舍去)或
(舍去)或![]() ,解得
,解得![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,所以
,所以![]() 的面积为
的面积为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,所以
,所以![]() 的面积为
的面积为![]() .
.
综上,![]() 的面积为4.
的面积为4.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(Ⅰ)应收集多少位女生样本数据?
(Ⅱ)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
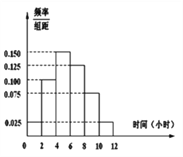
(Ⅲ)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
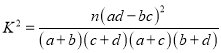
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲 | 82 | 82 | 79 | 95 | 87 |
乙 | 95 | 75 | 80 | 90 | 85 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的![]() 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温![]() (
(![]() )与该奶茶店的
)与该奶茶店的![]() 品牌饮料销量
品牌饮料销量![]() (杯),得到如表数据:
(杯),得到如表数据:
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程式
的线性回归方程式![]() ;
;
(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)
